Nun stehen also und in jedem Falle senkrecht aufeinander und die Schwierigkeiten, die uns einst die Binormale bereitete, sind fast beseitigt. Das „Fast” müssen wir noch erläutern: hat ein negatives Vorzeichen, was uns bei der Produktbildung von und zwangsläufig zu der unsinnigen Lösung einer negativen Energie führen würde. Wir hatten aber schon bei unseren Erklärungsversuchen der Richtungsquantelung des Diamagnetismus und der Supraleitung bereits festgestellt, dass die eigene Wechselwirkung - sofern sie nicht vernichtet werden will - entweder äußeren Feldern ausweicht - oder, wenn das nicht möglich ist, ein Gegenfeld aufbaut. Da wir aber unsere -Gleichung aus der Supraleitung entnommen haben, wo äußere Felder gemessen werden, dürfen wir nun für die eigene Wechselwirkung ohne große Skrupel das Vorzeichen von umkehren:

  XXXIX  

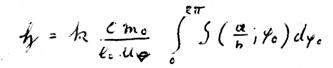
Wir schreiben nun noch einmal dazu:

  XL  

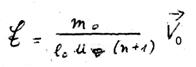
Beiden Gleichungen haftet ein Nachteil an. Beim -Feld haben wir diesen bereits über die Funktion diskutiert. Beim -Feld entsteht er durch folgenden Umstand: Wir haben uns vorgenommen, die eigene Wechselwirkungsenergie eines Teilchens zu berechnen, die letztendlich aus einem Produkt von und berechnet werden soll. Diese eigene Wechselwirkungsenergie soll eine Konstante sein, denn wir haben ja festgestellt, dass ein Teilchen nur mit der Größe eines Wechselwirkungsenergiequantums mit sich selbst in Wechselwirkung treten kann. Dieses Quantum sollte irgendwie mit dem Planck´schen Wirkungsquantum zusammenhängen, so dass man h berechnen kann. Nun kommen wir zu dem erwähnten Nachteil, der anhaftet: ist keine Konstante, weil variabel ist. Dadurch - so könnte man sagen - kann man auch kein Wechselwirkungsenergiequantum für die Energie erhalten. Dieser Widerspruch - ebenso wie der Widerspruch der im -Feld steckt - löst sich ganz einfach, wenn wir nur die bisher aufgestellten Aussagen konsequent anwenden: Es gibt bei eigener Wechselwirkung keine reine magnetische Energie - ebenso wie es keine reine elektrische Energie geben kann.