Sind die Rotverschiebungen des Lichtes entfernter Sternsysteme vollständig erklärt?

Einleitung:

Eine mathematisch korrekte Beschreibung einer Naturerscheinung führt zwangsläufig dazu, dass man über diese plausible oder triviale Angelegenheit nicht mehr nachdenkt. Wenn aber der gleiche Effekt durch einen ganz anderen Vorgang erzeugt wird, dann ist man natürlich geneigt, die bewährte und allgemein anerkannte Erklärung heranzuziehen, da der bekannte Zusammenhalt sich unwillkürlich vor den unbekannten (eventuell gut versteckten) drängt. Man hat ja gar keinen Anlass, anders zu denken. Dadurch wird der unbekannte Effekt nicht bemerkt und alle Beobachtungen werden auf dem bekannten physikalischen Vorgang zurückgeführt und ihre Deutung führt jetzt zwangsläufig zu falschen Aussagen.

Ganz kompliziert wird es dann, wenn beide Effekte gemeinsam auftreten und durch die Messung nicht unterschieden werden kann, was denn nun wohin gehört. Genau das ist aber bei dem o.a. Thema der Fall und bei der Unterscheidung wird sicherlich Staub aufgewirbelt, da hier zwei Beschreibungen konkurrieren.

Thema:

Wir betrachten also die Rotverschiebung von Spektren entfernter Sternsysteme, die durch den Doppler-Effekt erklärt wird und behaupten, dass neben dieser Erklärung noch eine zweite, bisher unbemerkte existiert. Der Doppler-Effekt führt zu Änderungen der Lichtwellenlänge, die sowohl Rot - als auch Blauverschiebungen sein können - je nach Geschwindigkeitsdifferenz zwischen Sender und Empfänger des Lichtes. Es existiert nun noch ein zweiter physikalischer Vorgang, der nur zu Rotverschiebungen von Spektren führt. Wir bezeichnen ihn "optisches Rauschen" und wollen ihn im Folgenden beschreiben: Wir untersuchen ein einzelnes Photon, das durch den Weltraum rast. Es besteht aus einer elektro-magnetischen Welle der Wellenlänge λ₀. Dieses Photon ist als Energiepaket der Energie E unterwegs.

$E=h\times {\nu }_0=\frac{h\times c}{{\lambda }_0}$

h	: Planck'sches Wirkungsquantum
ν0	: Frequenz des Lichtes
c	: Lichtgeschwindigkeit
λ0	: Wellenlänge der Welle

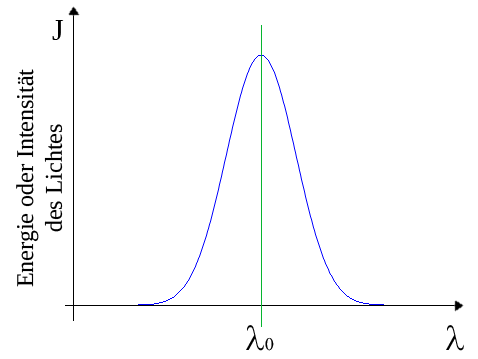
Dieses Photon muss eine Welle von endlicher Länge sein, sonst wäre eine Messung gar nicht möglich, denn der unendlich lange Wellenzug enthält keine Energie. Andererseits folgt aus dieser endlichen Länge des Wellenzuges, dass das Photon nicht streng monochromatisch sein kann, denn der streng monochromatische Wellenzug ist der oben erwähnte unendlich lange Wellenzug mit der Energie Null. Das bedeutet aber, dass neben der Messwellenlänge λ₀ in dichtem Abstand Energieanteile vorhanden sein müssen, wie in der Abb. 1 skizziert.

Dabei ist es nicht notwendig, den Intensitätsverlauf über λ genau zu kennen. Wichtig ist nur, dass ein Wellenlängenband (wenn auch sehr schmalbandig) im Photon enthalten sein muss:

$E=h\times \frac{c}{{\lambda }_0}~\underset{\mathrm{-\; \infty \; <!--INFINITY-->}}{\overset{\mathrm{+\; \infty \; <!--INFINITY-->}}{\int \; <!--INTEGRAL-->}}\mathrm{J(\lambda )}{d}_{\mathrm{\lambda }}$

J(λ)	: Intensität der Lichtwelle über λ
h	: Planck'sches Wirkungsquantum
c	: Lichtgeschwindigkeit
λ0	: Wellenlänge der Welle

Das Photon muss nun auf seinem sehr langen Weg durch eine riesige Anzahl von z.B. Wasserstoffatomen, denn es ist schon längst bekannt, dass der Weltraum nicht leer ist. Bei jeder dieser Durchquerung eines Atoms wechselwirkt die Welle mit demselben und zwar wird sie ein wenig verzögert, denn die Geschwindigkeit im Medium Wasserstoff ist etwas kleiner als im Vakuum.

Diese Wechselwirkung aber ist nun für die unterschiedlichen Intensitäten über λ verschieden, denn jede Welle findet (entsprechend ihrer Wellenlänge) die Inhomogenität unterschiedlich vor.

Dies geschieht natürlich nicht nur bei dem gewählten Beispiel der Wechselwirkung mit H-Atomen, sondern bei jeder Durchquerung von einzelnen Atomen oder Ionen. Natürlich ist dieser Effekt ungeheuer klein, aber er könnte durch die riesengroße Anzahl der Wiederholungen durchaus messbar werden. Trotzdem wird die Kritik vernichtend ausfallen: "Diese Haarspalterei kann doch keiner nachweisen!"
Dem darf aber entgegnet werden: Man kann durchaus die hier gemachten Behauptungen überprüfen, wenn man zur Kenntnis nimmt, das bei dem Verrauschen des Photons seine Energie erhalten bleibt. Denn mit der Wellenlängenvergrößerung geht eine Verbreiterung des spektralen Intensitätsverlaufes, also eine Bandbreitenvergrößerung einher.
Das bedeutet aber, dass die "verrauschten" Photonen ihre ursprünglich vorhandene Energie beibehalten haben.
Für eine messbare Überprüfung dieses Phänomens eignet sich natürlich der Photoeffekt: Die verrauschten Photonen sollten einen Photoeffekt zeigen, der ihrer ursprünglich ausgesandten Energie entspricht!

Vielleicht findet sich eine Institution, die das überprüft?