Now, and definitely stand vertically on top of each other and the difficulties once caused by the binormal are almost eliminated. But we have still to explain the „almost”: has a negative sign. This fact would inevitably provide the absurd solution of a negative energy when calculating the product of and . But in our attempts to explain the direction quantization of diamagnetism and superconduction, we have already found, that self-interaction - as far as it does not want to be eliminated - either avoids exterior fields or, if impossible, builds up a counter field. But as we have taken our equation from superconduction, where exterior fields are measured, for the self-interaction we may now reverse the sign of for the self-interaction:

  XXXIX  

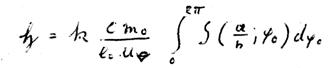
Again, we add :

  XL  

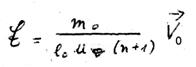
There is one drawback in the two equations. This drawback has already been discussed with the field for the function . In case of the field, the disadvantage is caused by the following situation: we have decided to calculate the self-interaction energy of a particle that shall ultimately be calculated from a product of and . This self-interaction energy has to be a constant because we have found that one particle can interact with itself only if it has the size of one interaction energy quantum. This quantum should somehow be related with Planck's constant, so that h can be calculated. Now we come to the abovementioned disadvantage of :
is not a constant because is variable. In other words, no interaction energy quantum can be obtained for the energy. This contradiction - like the contradiction inherent to the field - resolves very easily if we consequently apply the statements made above: in self-interaction there is no pure magnetic energy and no pure electrical energy as well.