Ein experimenteller Beitrag zum Ursprung der Masse

Es gibt zur Zeit keine Theorie, die Elektromagnetismus, Quantentheorie und Gravitation vereint, wenn man von nicht nachprüfbaren Hypothesen absieht. Das nachfolgend vorgestellte Experiment zeigt einen Ausweg aus dieser Krise der Physik. Es wird in diesem Experiment bewiesen, dass die Masse der Selbstinduktionsenergie von bewegten Ladungen zugeordnet werden muß. Der Nachweis gelingt mit einer hochempfindlichen Waage. Die in der Abbildung skizzierte Anordnung beschreibt den Versuchsaufbau:

Der Waagebalken besteht aus Glas und ist unten mit zwei gleich breiten und gleich dicken Streifen aus Aluminium beschichtet. Die Beschichtung erfolgte in einer Bedampfungscharge, sodaß keine Unterschiede zwischen den Al – Steifen entstanden, denn diese dienen als identische Strombahnen.

Die Balkenmitte ist auf zwei gleichen Stahlkugeln gelagert, die jeweils unter einer Al – Schicht die Stromzufuhr zur Gleichspannungsquelle (unten) herstellen.

Am Ende jedes Waagebalkens ist leitend verbunden mit dem Al – Streifen ein Toroid angebracht. Die beiden sonst gleichen Toroiden unterscheiden sich nur in dem Schraubensinn der Spulen. Der rechte Toroid entspricht einer Schraube mit Rechtsgewinde und der linke Toroid einer Schraube mit Linksgewinde.

Da ein sehr kleiner Effekt erwartet wird, dient ein Laserstrahl (rot) als Lichtzeiger. Dieser Laserstrahl wird in der Mitte des Waagebalkens von einer der Al – Schichten reflektiert und zeigt über einen festen Spiegel (oben) sehr empfindlich den Ausschlag der Waage an.

Die Waage wurde so aufgestellt, dass das Erdmagnetfeld parallel zu den Toroidenringen verläuft, um eventuelle störende magnetische Einflüsse auszuschalten.

Beim Einschalten des Stromes wurde ein deutlich messbarer Ausschlag der Waage erzielt. Dabei wurde der Toroid mit Rechtsgewinde leichter und der Toroid mit Linksgewinde schwerer.

Beim Umpolen des Stromes entstand der gleiche Ausschlag des Waagebalkens: Wieder wurde der Toroid mit Rechtsgewinde leichter als sein Gegenüber.

Wenn man den gesamten Waagebalken mit den Toroiden abnahm und seitenverkehrt wieder auflegte, sodaß sich nun der Toroid mit Rechtsgewinde links befand und sein Gegenstück rechts, dann stellte man fest, dass jetzt der Waagenausschlag beim Einschalten des Stromes entgegengesetzt erfolgte. Das bedeutete, dass wieder der Toroid mit Rechtsgewinde leichter wurde als sein Gegenstück auf der anderen Seite – übrigens auch diesmal unabhängig von der Stromrichtung.

Wir hatten gewissermaßen die Massenänderungen mit dem Schraubensinn mitgenommen.
Für Nachprüfungen des Experimentes werden hier die Messbedingungen angegeben:

Waagebalken:

- Floatglas, beidseitig blank, 500mm x 20mm x 2mm

- Al – Beschichtung 2 Streifen, je 8mm breit, 2µm dick

- unbeschichteter Zwischenraum: 4mm breit

- Auflagekugeln aus Stahl: 3,9mm

Toroiden:

- Füllmaterial jeder Ringspule: Polystyrol – Schaum, nichtleitend

- Gewicht eines Polystyrol – Ringkörpers: 4,3 Gramm

- Abmaße der Polystyrol – Schaum – Ringe:

* Ring – Durchmesser innen: 95mm

* Ring –Durchmesser außen: 145mm

* Ø der Polystyrol – Körper: 50mm

- Anzahl der Windungen auf jedem Toroiden: 135

- Durchmesser des Wicklungsdrahtes: 0,6mm

- Material des Wicklungsdrahtes: Aluminium

- Gesamt – Gewicht des Drahtes eines Toroiden: 85,6 Gramm

Laser:

- He – Ne – Laser mit λ = 633nm

- Lichtzeigerweg insgesamt: 4,8m

Stromdaten:

- Gleichstrom, 400 mA

Waagen – Eichung:

- Durch Auflegen von mg – Gewichten wurde der Ausschlag der Waage geeicht

Messergebnis:

Bei 400 mA wurde eine Waagebalkenseite um mindestens 0,1 mg leichter und die gegenüberliegende um mindestens 0,1 mg schwerer.

Zusammenfassung:

1. Die Masse erzeugen bewegte Ladungen durch Selbstinduktion.
2. Die hierbei entstehende Energie wird von der Geometrie der Bewegung dieser Ladungen bestimmt und ist damit an den Ort der Bewegung gebunden, gewissermaßen gespeichert. Dieser fixierten Energie muß die Masse zugeordnet werden.
3. Nicht nur Gruppen von bewegten Ladungen, sondern auch einzelne Ladungen müssen durch Selbstinduktion Masse erzeugen, da sie bei Bewegung mit ihrem eigenen Feld wechselwirken.
4. Diese Selbstinduktion einzelner Ladungen öffnet die Tür zum Verständnis der Quantentheorie

Das Experiment inspiriert durch: B. Heddisch, Betrachtungen zum Thema Atom »

Die vorliegenden

"Betrachtungen zum Thema Atom"

wurden am 04. Oktober 1972 abgeschlossen und vom Verfasser unterzeichnet.


Für den Inhalt ist ausschließlich der Verfasser verantwortlich.

Technischer Dienstleister

spezialist.it
Sven Heinrich
  atom(at)heinrichcomputer.de



Albert Einsteins berühmte Worte
"Gott würfelt nicht!"
haben diese Arbeit ausgelöst.

Nach einigen tastenden Schritten bzw. Fehltritten fanden sich am Wegrand verblüffend einleuchtende Erklärungen zum Pauli-Prinzip, zur magneto-mechanischen Anomalie (Spin), zur Heisenberg'schen Unschärferelation, zur Dualität von Welle und Teilchen sowie zum Problem der universellen Naturkonstanten.
Ermutigt durch diese Anhaltspunkte wurde herausgefunden, dass das Planck’sche Wirkungsquantum keine universelle Naturkonstante sein kann, sondern dass es den Ursache-Wirkungs-Komplex einer Ladung mit sich selbst beschreibt. Mit anderen Worten: Eine Ladung kann im Atom mit sich selbst in Wechselwirkung treten, indem sie mit ihrem eigenen elektromagnetischen Feld wechselwirkt.
Mit Hilfe dieses Postulates gelang es, den Wert des Planck’schen Wirkungsquantums mit guter Näherung zu berechnen.
Im folgenden Fortschreiten auf diesem Wege werden eigene Wechselwirkungsmechanismen entworfen, die Elementarteilchen, wie Proton, Neutron usw., darstellen und die die Kernkräfte als gekoppelte eigene Wechselwirkungsenergien beschreiben. Dabei stellt sich heraus, dass das Masse-Energie-Äquivalent E=m₀C² durch solche eigenen Wechselwirkungen erzeugt wird.

Im abschließenden „Phantastischen Ausblick“ wird bemerkt, dass interessante und neue Perspektiven des Naturverständnisses entstehen können.



Seit der Einführung der Bohr´schen Postulate hat die Quantentheorie eine große Anzahl von Naturerscheinungen richtig gedeutet und vor allem mathematisch einwandfrei beschrieben.

Dieser modernste Zweig der physikalischen Wissenschaft hat heute ein derartiges Ausmaß angenommen, dass es wohl kaum für einen Einzelnen gelingen dürfte, auch nur annähernd einen vollständigen Überblick über alle - von der Quantentheorie beherrschten Wissensgebiete zu erlangen. Oft sind Jahre der .Ausbildung notwendig, um einen Physiker in einem der vielen Spezialgebiete zum Fachmann werden zulassen.

Betrachtet man nun das Entwicklungstempo der Quantentheorie, so muss man feststellen, dass die Zeit der großen und schnellen Fortschritte vorbei zu sein scheint, denn jede neue Erkenntnis wird wohl doch mit großem experimentellem und rechnerischem Aufwand erkauft und die Diskussionen um neue Hypothesen scheinen mehr und mehr Zeit zu beanspruchen.

Ebenfalls erhält man den Eindruck, dass verschiedene experimentelle Ergebnisse die Quantentheorie vor schwierig zu lösende (oder vielleicht sogar im Rahmen dieser Theorie vor unlösbare) Aufgaben stellen.

Vielleicht hat die Quantentheorie tatsächlich eine Grenze erreicht, die es einfach nicht mehr gestattet, wesentliche Fortschritte bei der Erkennung der Natur zu erzielen?

Wenn aber das der Fall ist, dann darf man erwarten, dass die Grundpfeiler dieses großen theoretischen Gebäudes nicht fest genug gebaut sind, um den Aufbau zu tragen und man muss vielleicht noch einmal ganz von vorn beginnen.

Die vorliegende Arbeit verfolgt ein solches Ziel. Sie will Zweifel an der Richtigkeit der Grundlagen der Quantentheorie erzeugen, denn gerade diese Grundlagen tragen für den Laien fast ausnahmslos scheinbare Widersprüche in sich. Dazu zählt der Dualismus des Lichtes und der Dualismus der Teilchen (denen man ja auch ein Wellenpaket zuordnen kann, das aber eigentlich sofort zerfließen müsste). Dazu kann man den Eigendrall (Spin) der Elektronen zählen, der ja so groß sein müsste, dass sogar die von der Relativitätstheorie geforderte höchste Geschwindigkeit - die des Lichtes - um ein Vielfaches überboten wird. Ebenso existiert im Bereich der Quantentheorie die berühmte Unschärferelation, die jedes Eindringen über eine gewisse Grenze hieraus verbietet usw.



Diese "Widersprüche" sind für den Fachmann keine Widersprüche, denn die Quantentheorie geht ja davon aus, dass es keine Kausalität der einzelnen Naturvorgänge gibt, lediglich existiert im Rahmen dieser Theorie eine Kausalität von Wahrscheinlichkeiten, ja es lässt sich auf dem Boden dieser Theorie sogar nachweisen, dass überhaupt kein anschauliches - also kausales - Modell des Atoms existiert.
Vielleicht ist aber gerade dieser Standpunkt einer kritischen Bearbeitung würdig, denn eigentlich basiert jede klassische Beschreibung auf dem Kausalitätsprinzip und dieses Prinzip, das durch die. Erfahrung vielfach bestätigt wird, benutzt ja auch soweit als möglich die Quantentheorie.

Nehmen wir nun einmal an, jemand würde behaupten, dass dieses Prinzip für alle Naturvorgänge gilt. Sogleich würde jeder Fachmann eine solche Behauptung mit einer Vielzahl von Beweisen widerlegen können.

Nehmen wir aber nun weiterhin an, dass wirklich die Natur sich in allen Details kausal verhält, dass sogar alle Beweise, die gegen eine solche Auffassung stehen, richtig sind und dass nur der Standpunkt, von dem aus diese Beweise geführt werden, einer Revision bedarf, dann entsteht ein eigentümlicher Widerspruch: Erstens ist nun jedem Fachmann der Weg für eine Weiterentwicklung dieser Theorie wegen der oben angegebenen zahlreichen Beweise versperrt. Zweitens wäre nun zwar der Laie in der Lage, einen kausalen Standpunkt zu beziehen, aber er ist in keinem Falle den Argumenten des Fachmannes gewachsen, weil er eine derart dürftige Kenntnis der Quantentheorie besitzt, dass er den Gegenargumenten nicht gewachsen ist. Andererseits aber entsteht nun für den Laien (im Interesse der Weiterentwicklung der Wissenschaft) trotz aller Unzulänglichkeit der Beweisführung, die Verpflichtung, diesen Standpunkt zu vertreten.

Deswegen fordert der Verfasser für sich das Recht, einen kausalen Standpunkt zu beziehen und diesen nicht streng zu beweisen. Der Leser möge also die folgenden heuristischen Betrachtungen lediglich als eine Meinung und ein (vielleicht interessantes) Abenteuer auffassen, sowie die für einen solchen Standpunkt notwendigen Willküren verzeihen.

Der Weg

Am Anfang dieser Betrachtung soll eine Frage stehen, die an die kritischen Bemerkungen der Einleitung anschließt. Es ist bekannt, dass man sehr gut und übersichtlich die Abstrahlung einer elektromagnetischen Welle eines Herz'schen Oszillators beschreiben kann. Jedoch versagt diese Vorstellung sofort, wenn man ein anschauliches und übersichtliches Modell der Abstrahlung eines Lichtquants aus einem Atom angeben will. Dies ist eine der Eigentümlichkeiten der Quantentheorie. - Andererseits können wir, wenn wir die Produkte beider Abstrahlungsmechanismen (nämlich die elektromagnetischen Wellen) betrachten, einfach keinen wesentlichen Unterschied entdecken und fragen deshalb mit vollem Recht: Warum soll bei einem physikalischen Objekt, das durch zwei verschiedene Herstellungsverfahren erzeugt wurde, nur in einem der beiden Fälle die Art der Herstellung überschaubar sein und beim zweiten nicht? Diese Frage ist für uns nur Hilfsmittel, um in das Gebiet der Quantentheorie von einer anderen Seite her (als der üblichen) einzudringen. Wir beschreiten also einen solchen Weg, der es uns gestattet, ein kausales Bild der Natur zu entwerfen und beginnen mit den Gleichungen, die den Abstrahlungsmechanismus eines Atoms regieren.

Es sei vorausgeschickt, dass bei der Behandlung unseres Themas nicht das Bedürfnis besteht, jedes Zeichen oder Symbol genauestens zu erläutern, denn diese Erläuterungen stören im allgemeinen den Gedankenfluss. Stellvertretend dafür soll lediglich das Bemühen bestehen, möglichst die Zeichen zu verwenden, die jeder Leser/in einem Physikbuch findet und, wenn nötig, sollen anschauliche Zeichen eingeführt werden.
Wir betrachten nun folgende Gleichungen:

(Energie eines Lichtquants)

(Gleichung der Geschwindigkeit des Lichtes)





und

  III  
    (Differenz der Energieniveaus zweier um einen Kern „kreisender” Elektronen)

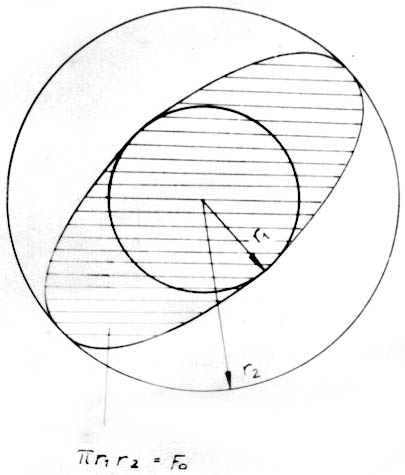
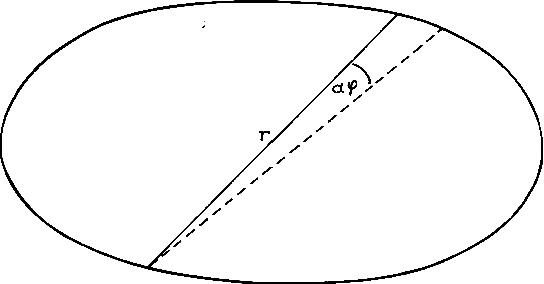
Daraus folgt, wenn man 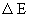eliminiert und mit erweitert (Abb. 1):

  IV  

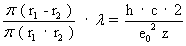
oder:

  V  

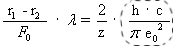
Auf der rechten Seite steht nun im umrandeten Feld im Wesentlichen die Sommerfeld'sche Feinstrukturkonstante; auf der linken Seite wird die Gleichung recht interessant. Hier steht das Verhältnis zweier geometrischer Größen, multipliziert mit der Wellenlänge des ausgestrahlten (oder absorbierten) Lichtes. Sollte etwa die Kurve, die die Ellipsenfläche umrandet, die Bahn sein, auf der das Elektron umläuft, während es zur Abstrahlung des Lichtquants kommt?

Verschiedenes spricht hierfür - erstens die Tatsache, dass im Zähler links die Differenz zweier Radien (eine Höhendifferenz) steht. Wir verbinden mit der Höhendifferenz die Vorstellung der Differenz zweier elektrischer Größen. Zweitens steht im Nenner eine Fläche, die jeder Physiker mit einem Magnetfeld in Verbindung bringt. Ja, man ist direkt versucht, hier den Abstrahlungsmechanismus zu ergründen, wenn man sich vorstellt, dass das Elektron zwischen beiden (strahlungslosen) Bahnen auf der Ellipsenkurve pendelt, bis seine Energiedifferenz verbraucht ist und es auf eine der beiden Bahnen einschwenkt. Beim "Sturz" oder "Steigen" sollte es dabei ein elektrisches Feld abstrahlen; beim Erreichen der höchsten Geschwindigkeit (also beim Tangieren der inneren Bahn) ein magnetisches Feld.





Doch eigentlich war dies nicht das Ziel unserer Betrachtungen; wir wollen mit kleinen Umformungen einen anderen Blickwinkel gewinnen. Wir benutzen folgende Größen:

  VI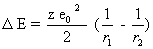  

Daraus folgt:

  VII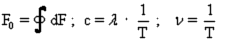  

Diese Umrechnung hatte zum Ziele, die Sommerfeld'sche Feinstrukturkonstante von dem c zu befreien, denn es ist bekannt, dass man dann die Geschwindigkeit des Elektrons dem auf der innersten Bahn des Wasserstoffatoms erhält, die bei unserer Rechnung mehr Vorstellung und Anschaulichkeit bietet. Im Nenner steht also nun die Geschwindigkeit des Elektrons auf der untersten Bahn des Wasserstoffatoms.

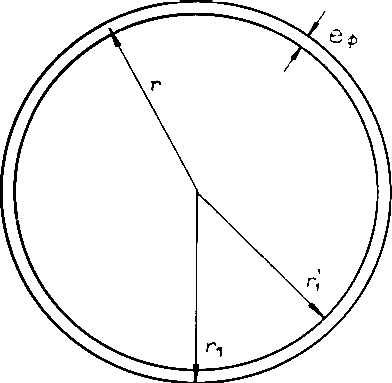
Betrachtet man nun aufmerksam Gleichung VII und lässt einmal die Phantasie spielen, dann darf man fragen: Wenn Gleichung VII die Gleichung des Abstrahlens ist, wie sieht dann die Gleichung einer festen Bahn aus? Hier wird über eine geschlossene Fläche integriert, vielleicht muss bei einer festen Bahn über eine Ringfläche integriert werden? Wir versuchen es, denn solch ein Versuch kostet nicht mehr als einen Misserfolg. Wie oft ist aber schon gerade durch falsches Rechnen ein vernünftiger Gedanke entstanden! Wir ersetzen also den Nenner durch solch ein Integral über eine Ringfläche (Abb. 2):

  VIII       Für muss der Durchmesser des Elektrons ( eØ ) herhalten.



Daraus folgt für den Nenner der linken Seite:

  IX  

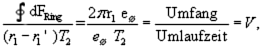
eine Umlaufgeschwindigkeit auf einer festen Bahn. Das ist verblüffend!
Setzen wir nun in Gleichung VII z = 1 und vergleichen beide Nenner, so steht nun da:

  X  

auf der innersten Bahn des Wasserstoffatoms!

Nun kommen wir zu der entscheidenden Frage, denn alles das, was bisher aufgeschrieben wurde, diente zur Erarbeitung der nun folgenden Sätze. Wir fassen zusammen (unter der Voraussetzung, dass unsere bisherigen Vermutungen einen wahren Kern enthalten): Liegt der Atomkern innerhalb der zu integrierenden Fläche, dann wird Licht emittiert (oder absorbiert). Liegt dagegen der Kern nicht in dieser Fläche, dann haben wir es mit einer festen Bahn zu tun. Warum also integriert man nicht in jedem Falle über den Kern?

Da wir schon weiter oben die Fläche mit dem Magnetfeld identifizierten, behaupten wir nun:

Das Magnetfeld, das ein Elektron bei einem Umlauf auf einer stationären Bahn (die der Quantenbedingung genügt) erzeugen sollte, ist am Kern einfach Null, es ist nicht da. Wenn aber das Magnetfeld am Kern nicht da ist, kann natürlich solch ein Elektron bei seinem Umlauf nicht strahlen, muss also auf einer stabilen Bahn bleiben, denn zum Abstrahlen von Lichtquanten braucht man ein elektrisches und ein magnetisches Feld. Vielleicht läuft also das Elektron auf einer Bahn um den Kern, die so geartet ist, dass am Kern einfach kein Magnetfeld entsteht. Da aber der Kern durch die Coulomb-Anziehung das Elektron auf eine Kreisbahn oder Ellipse bannt, gibt es für die Auswahl verschiedener Bahnkurven zunächst gar keine Möglichkeit, irgendwie anders geartete Bahnen als Kreise oder Ellipsen zuzulassen.





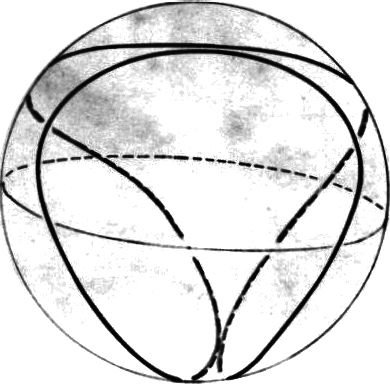
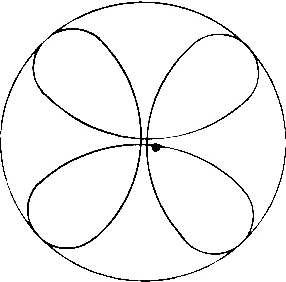
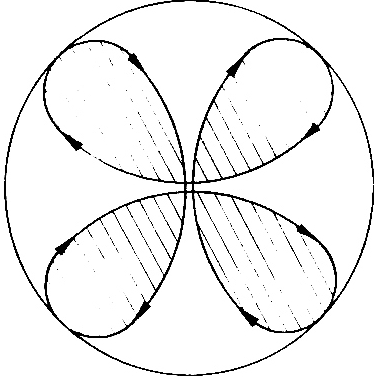
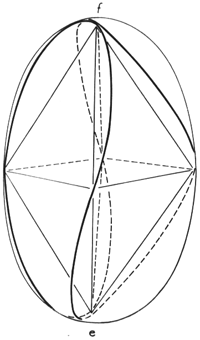
Andererseits aber berechnet die Quantentheorie für den einfachsten Fall der innersten Bahn des Wasserstoffatoms eine kugelsymmetrische Ladungsverteilung. Aus diesem Grunde (- oder besser: Anhaltspunkt -) lassen wir nun auch für die Auswahl geeigneter Bahnkurven die ganze Kugeloberfläche, deren Radius gleich dem der Kreisbahn sein soll, zu. Wir beschränken uns also auf den einfachsten Fall, nämlich auf die Bahnkurve des Elektrons auf der innersten Bahn des Wasserstoffatoms. Dabei lassen wir das Elektron mit der konstanten Geschwindigkeit - die die Quantentheorie auf dieser Bahn fordert - umlaufen, nur lassen wir zu, dass das Elektron seitlich abgelenkt werden kann und kümmern uns zunächst noch nicht darum, wodurch das Elektron denn aus einer ebenen Bahnkurve (Kreisbahn) heraus getrieben werden kann. Am besten eignet sich für solch ein Vorhaben eine hohle Glaskugel. Als Vorschlag für eine solche Bahn soll die in der Abbildung 3 gegebene Bahnkurve gelten. Vier Kleinkreise umlaufen die Kugelfläche so, dass sie stetig ineinander übergehen.

An dieser Stelle begehen wir den ersten Willkürakt. Wir fordern nämlich, dass der Drehimpulserhaltungssatz für diese Bahn nicht mehr gelten soll. Wohl lassen wir noch zu, dass der zahlenmäßige Wert des Drehimpulses konstant bleiben soll, aber wir fordern, dass die Richtung des Drehimpulsvektors keine Konstante mehr sein soll. Wir befinden uns damit in vollem Widerspruch zur Quantentheorie, ja mehr noch: Die Konstanz des Drehimpulsvektors (erzeugt noch durch die verschärfte Vorschrift durch das Planck´sche Wirkungsquantum) ist ja gerade die Grundlage aller Theorien über die Elementarteilchen. Hier an dieser Stolle ist auch einer der Hauptwidersprüche der Quantentheorie: Sie fordert Konstanz des Drehimpulses und berechnet kugelsymmetrische Ladungsverteilung! Man kann diese Stelle als Scheideweg bezeichnen. Entweder man entscheidet sich für den Drehimpuls und erhält eine nichtkausale Welt - oder man entscheidet sich für die kugelsymmetrische Ladungsverteilung und versucht den Aufbau einer kausalen Welt. Wir entscheiden uns für den zweiten Weg und in diesem Sinne fassen wir unseren Schritt zum Übergang auf eine solche Bahn als keinen Willkürakt auf.

Betrachtet man diese Bahn vom Mittelpunkt der Kugel aus, also aus der Sicht des Kernes, so stellt man fest, dass zwar vier gekrümmte tropfenförmige Flächenstücke zu sehen sind, wobei jedes umlaufene Flächenstück ein Magnetfeld am Kern erzeugen könnte.



Fordert man aber den folgenden Satz, dann kann am Kern wirklich kein Magnetfeld entstehen:

Ein Magnetfeld wird nur in einer solchen Richtung des Raumes bemerkt, in der eine Ladung eine stetige und in der räumlichen Ableitung stetige geschlossene Kurve beschreibt.

Da aber keines der vier Flächenstücke in der räumlichen Ableitung der Bahnkurve (aus der Sicht des Kernes) stetig ist, wäre tatsächlich am Kern „magnetische Windstille”. Im Übrigen herrscht diese „Windstille” im gesamten Innenraum der Kugel. Diese Forderung (im Folgenden „Magnetfeldsatz” genannt) ist nun wirklich nicht allzu einschneidend, wenn man bedenkt, dass das magnetische Feld ein Wirbelfeld ist.

Ein Wirbel dürfte aber nur dann entstehen, wenn der Erzeuger - die Ladung - eine stetige und in der Ableitung stetige geschlossene Kurve beschreibt, auf anderen Wegen ist die Erzeugung eines Wirbels bei Reibungsfreiheit unvorstellbar. Im Übrigen steht dieser Satz auch nicht im Widerspruch zur makroskopischen Erfahrung. Wir vermuten also, dass die größten Unsicherheiten der Quantentheorie hei der Deutung von magnetischen Effekten bestehen.

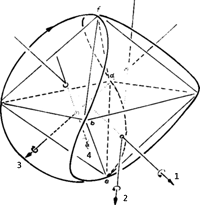
Doch zunächst wollen wir den Radius der 4 Kleinkreise angeben. Dazu betrachten wir die Abbildung 4.

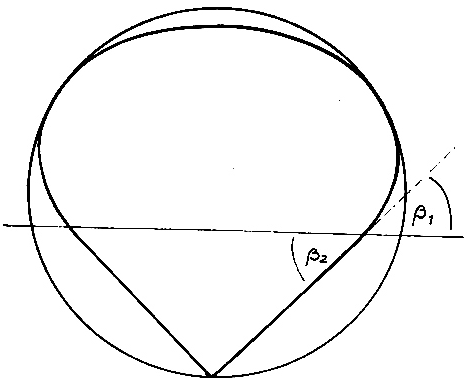
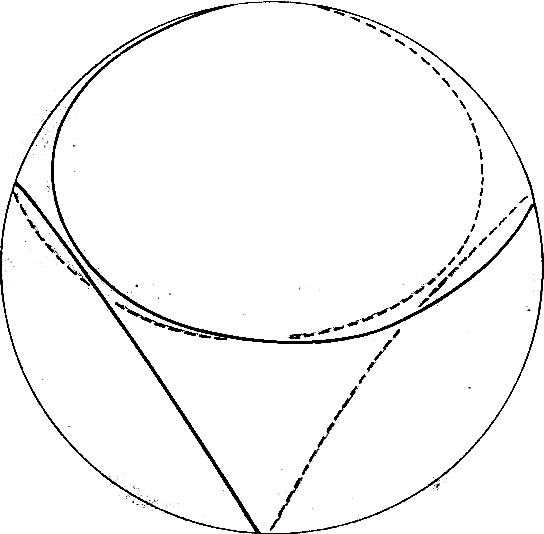
(Es sei hier darauf hingewiesen, dass der Leser, der eine hohle Glaskugel zur Hand hat und, diese Bahn nachzeichnet, sehr gut beraten ist. Er durchschaut die nun folgenden Erläuterungen im wahrsten Sinne des Wortes). Wir blicken zuerst in Richtung e - f (Abb. 5). Die Bahnkurve nimmt die Form einer Rosette an, deren vier Teile jeweils aus dem Kurvenast einer Ellipse bestehen. Wir lassen nur noch eine Ellipse zu und berechnen aus der Schar von Ellipsen, die durch den Koordinatenursprung gehen und den einhüllenden Kreis berühren diejenige Ellipse, die mit dem Kreis und der Geraden x = y einen gemeinsamen Punkt besitzt (Abb. 6). Die große Halbachse dieser Ellipse ist gleich dem Radius der Kleinkreise unserer Bahnkurve.

  IX  
    R = Radius der Kugel

Dass diese Bahnkurve (betrachtet aus Richtung e - f) stetig und in der Ableitung stetig ist, bedarf keiner weiteren Erläuterung, denn ihre Berechnung erfolgte unter dieser Bedingung. Zum Nachweis der Knickfreiheit über die ganze Kugelfläche hinweg müssen wir noch aus zwei anderen Richtungen auf diese Kurve sehen und hier die Stetigkeit der Ableitungen überprüfen. Es genügt, wenn dies für die Richtung a - b nachgewiesen wird; wenn hier die Stetigkeit der Ableitung gezeigt werden kann, ist diese mit der dritten unabhängigen Sicht identisch (z.B. b - c). Es gelingt leicht, zu zeigen, dass ist. (Abb. 7).

Wir haben nun also eine überall stetige und knickfreie geschlossene Raumkurve vor uns, die einem Oktaeder umbeschrieben ist, der in der Kugel Platz gefunden hat. Wir haben außerdem die von der Quantentheorie geforderte kugelsymmetrische Ladungsverteilung erreicht, wenn wir das Elektron (zunächst zwangsweise) auf dieser Bahn herumführen. Diese Bahn ist stückweise eben.

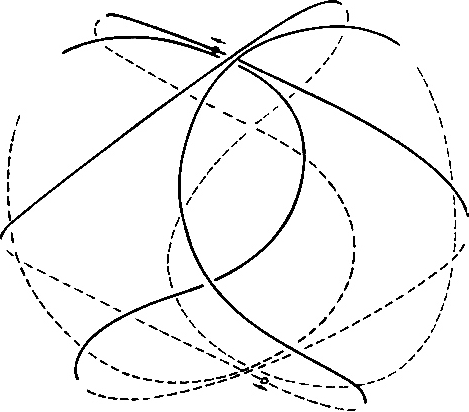
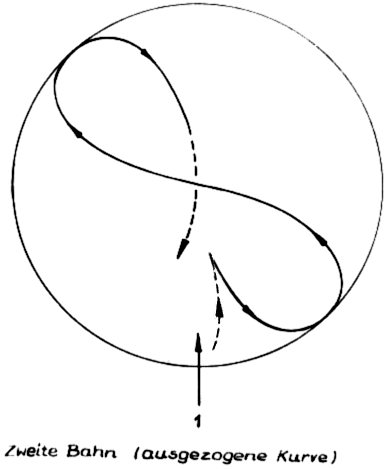
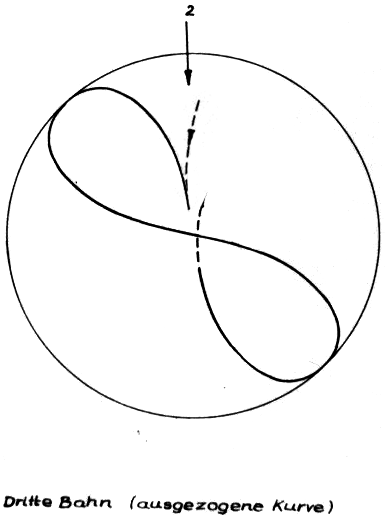
Nun gehen wir frischen Mutes an die Beantwortung der Frage, wodurch denn das Elektron zu dieser Taumelei veranlasst werden soll. Es muss auf jeden Fall eine Kraft sein, die keine Arbeit (also keine Geschwindigkeitsänderungen) leisten soll; lediglich Richtungsänderungen sollen erlaubt sein. Das ist - wir vermuten es - sicherlich die Lorentzkraft und wir schauen uns nach Magnetfeldern um. Diese sind auch da - denn wir brauchen nur in Richtung der Pfeile 1, 2, 3 oder 4 zu sehen, dann erblicken wir stetige - und in der räumlichen Ableitung stetige geschlossene Ellipsen, die nicht im Widerspruch zu unseren anfangs formulierten Magnetfeldsatz stehen. Sollte etwa das Elektron auf seinen eigenen Magnetfeldern schwimmen - ohne dass der Kern etwas davon merkt (Abb. 8)?

Das wäre also die Erklärung für die stehenden Materiewellen, die bisher als ein Modell für die Vorstellung der festen Bahnen herhalten mussten. Diese "stehenden Wellen" würden sich also als drehende Magnetfelder entpuppen.

Diese Vorstellung der drehenden Magnetfelder ist die erste erfolgreiche Anwendung unseres Modells auf die tatsächlichen - von der Natur vorgegebenen Verhältnisse. Wir werten sie als Indiz für die Richtigkeit des Modells und schauen uns (bevor wir an die Beantwortung der Frage nach der Ursache der Taumelei des Elektrons gehen) zunächst nach weiteren Indizien um. Wir beschreiten diesen Weg des Vorauseilens nur deshalb, weil wir doch prüfen wollen, ob das angegebene Bahnmodell noch mehr solcher Indizien liefert, die ein anschauliches, zwangloses Bild der Naturvorgänge geben - und damit sich die weitere Betrachtung überhaupt lohnt. Wir stellen also die Frage: Wie viel Elektronenbahnen dieser Art können wir auf solch einer Kugelschale zulassen, wenn die Kernladungszahl entsprechend vergrößert wird? Wir nahmen an, dass das Elektron auf seinem eigenen Magnetfeld schwimmt. Deshalb müssen wir nun sagen: Nur noch ein zweites Elektron passt auf die Kugelschale (Abb. 9). Dieses zweite Elektron muss in jedem Punkt der Bahn gegenüber dem ersten stehen (es soll also hinter dem Kern so versteckt sein, dass sich beide Elektronen nicht "sehen"). Jedes weitere Elektron, das hinzukommt, würde nun dieses schöne Versteckspiel beenden und nach dem Magnetfeldsatz die Magnetfelder der anderen beiden Elektronen "bemerken". Die Harmonie wäre zu Ende und die stationäre Bahn wäre gesprengt.

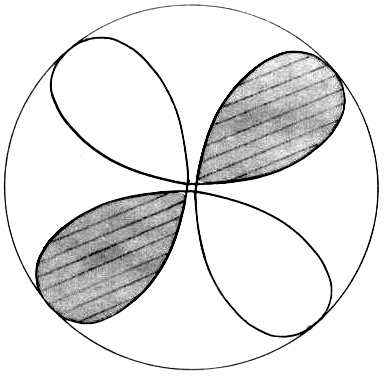
Das ist eine anschauliche Deutung des Pauli-Prinzips. Doch wir müssen noch etwas nachholen. Wir sind noch eine anschauliche Deutung des Elektronenspins schuldig, denn ohne den „Spin” kennen wir das Pauli-Prinzip nicht erläutern. Es ist ja bekannt, dass der eingeführte Spin das Elektron in solch gewaltige Drehung versetzen soll, dass man mit der Relativitätstheorie in Konflikt kommt. Die von uns eingeführte Bahn aber kommt mit niedrigeren Geschwindigkeiten aus. Wir schauen wieder einmal in Richtung e - f und erblicken ein durch 4 umlaufene Blätter erzeugtes Magnetfeld, das wiederum nicht in Widerspruch zu unserem Magnetfeldsatz steht (Abb. 10). Das ist der Spin.

Da nach unserer Versteckspiel-Theorie für zwei Elektronen diese Rosettenfläche von beiden Elektronen im umgekehrten Drehsinn umlaufen wird, erhalten wir also hier das richtige Resultat für die antiparallele Stellung der Spinmagnete beim Edelgas Helium im Grundzustand.

Doch nun sind wir verpflichtet, das gyromagnetische Verhältnis des Einstein- de Haas-Versuches für unser Spinmodell auszurechnen, um zu zeigen, dass dieses Modell auch hier Übereinstimmung mit den tatsächlich gegebenen Werten liefert:

  XII  

    Das magnetische-Moment ist (gemittelt über die Dauer eines Umlaufes):

Daraus folgt:

  XIII  

Der Drehimpuls (ebenfalls über einen Umlauf gemittelt) ist:

  XIV  

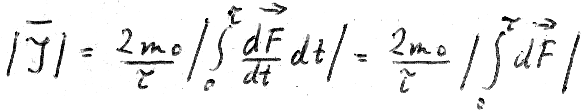
auf Wir behaupten nun, dass das Integral 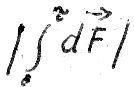gleich 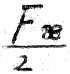ist.

Man kann diesen Beweis auf verschiedene Weise führen, z.B. dadurch, dass man die Tatsache berücksichtigt, dass der (gemittelte) Drehimpuls sich aus zwei Drehungen zusammensetzt: Eine Vorwärtsdrehung innerhalb jedes Quadranten und eine Rückwärtsdrehung beim Wechsel von einem Quadranten in den anderen. Wir führen den Beweis mit Hilfe einer sehr anschaulichen Hilfsbahn. Wir können nämlich die angegebene Bahn durch drei einzelne Bahnen ersetzen, deren mittlerer Drehimpuls sich sofort aus der Bahnkurve ablesen lässt, so dass wir ohne große mathematische Hilfsmittel auskommen. Der erste Teil dieser Bahn ist in der Abbildung 11 angegeben.

Wir lassen also das Elektron mit genau der Geschwindigkeit, die es auf einem äquivalenten Punkt der ursprünglichen Bahn hatte, umlaufen; nur lassen wir es nicht durch den Mittelpunkt der Rosette hindurch tauchen, sondern stoppen es hier augenblicklich, um es mit der gleichen Geschwindigkeit in den nächsten Quadranten zu schicken (der Anschaulichkeit halber sind die Bahnen nicht bis in den Mittelpunkt gezeichnet worden).

Wir haben nun im zweiten und vierten Quadranten einen Fehler gemacht und korrigieren diesen sogleich durch die zweite und dritte Bahn; indem wir an den Stellen 1 und 2 die erste Bahn aufschneiden und die zweite und dritte Bahn dazwischen fügen (Abb. 12 u. Abb. 13):
All diese Manipulationen sind zulässig, weil wir in den Momenten die Bahnveränderungen vornehmen, in denen der Beitrag zum Drehimpulsintegral Null ist.

Daraus folgt nun offensichtlich, daß der mittlere Drehimpuls der ersten Bahn gleich 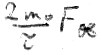sein muß. Für die beide anderen Bahnen ergibt sich der mittlere Drehimpuls 0, was man unschwer erkennen kann. Für das vollständige Ablaufen unserer aus drei Hilfsbahnen bestehenden Konstruktion brauchen wir aber die doppelte Zeit, die sonst für die tatsächlich gegebene Rosettenbahn gebraucht wird.

Wir haben also bei unserer Hilfsbahn offensichtlich den mittleren Drehimpuls einer zweimal abgelaufenen tatsächlichen Bahn erhalten. Daraus folgt sofort:

  XV  

Daraus folgt, daß bei einem solchen "Vorwärtsdrall mit Rückwärtsgang" nur die Hälfte der Fläche zur Flächengeschwindigkeit beitragen kann (Abb. 14).
Aus XIII und XV folgt nun das gyromagnetische Verhältnis des "Spin":

  XVI  

Nun dürfen wir also für unser Modell in Anspruch nehmen: Es gibt keinen Elektronendrall im Sinne der Quantentheorie.

Jetzt kommt auch langsam Klarheit in die Frage, warum beim Stern-Gerlach-Experiment eine Richtungsquantelung auftritt. Ganz einfach deshalb, weil die Elektronen nicht gern bei ihrem feingewebten Magnetfelddrall gestört sein wollen. Ebenso wie sie es ablehnen, einen dritten Partner in eine Kugelschale mit aufzunehmen, lehnen sie es ab, von äußeren Feldern in ihrem Rythmus gestört zu werden. Das gelingt am besten, wenn sie die Achse e - f in Richtung des äußeren Feldes drehen, dann sind alle 4 Magnetfelder gleichberechtigt und keines ist gegenüber den anderen 3 im Vorteil. - Noch ein Argument spricht gegen die Existenz des Elektronendralls im Sinne der Quantentheorie: Es ist nicht bekannt, dass freie Elektronen - z.B. Kathodenstrahlen oder Elektronen, die beim
ß-Zerfall der Radioaktivität entstehen - einen Stern-Gerlach-Effekt zeigen. Andererseits hat es wenig Sinn, gegen eine Vorstellung anzukämpfen - die ja gar nicht von sich behauptet, anschaulich zu sein, denn der Spin des Elektrons sollte ja nur ein Ersatzmodell für Vorgänge sein, die im einzelnen nicht angegeben werden können. Ebenso erhebt das Atommodell der Quantentheorie - bis auf die mathematisch einwandfreien Aussagen keinerlei Anspruch auf Anschaulichkeit - so daß man bei dem Vorhaben der Diskussion der Nachteile des bisherigen Modells sehr leicht offene Türen einrennt, weil dieses Modell nicht exisitert.

Nun wenden wir uns wieder der Frage zu, die wir bisher nicht beantwortet haben. Die Vermutung lautete, daß die Lorentz-Kraft dafür verantwortlich sein kann, dass das Elektron auf seiner Bahn diese Taumelei veranstaltet. Wir nehmen also das Elektron vorsichtig an die Hand und führen es entlang der vier Kleinkreise. Danach versuchen wir - eines der vier Magnetfelder (Richtung 1 zum Beispiel) zu berechnen und berechnen dann die Lorentz-Kraft, indem wir , bilden. Danach sollte diese Lorentz-Kraft gleich der auf den Kleinkreisen wirkenden Zentrifugalkraft gesetzt werden. Nun wird es spannend:

Wenn eine solche Gleichung gewonnen werden kann, dann kann man daran denken, das Planck´sche Wirkungsquantum zu berechnen. Denn durch die Gleichheit von Zentrifugalkraft und Coulomb-Anziehung des Kernes existiert ja eine zweite Bestimmungsgleichung, die das Elektron auf die Kugelschale bannt - und diese Gleichung enthält - wegen der "Quantelungsvorschrift" h!

Es sei dahingestellt, dass wir sogleich auf dem angegebenen Wege Erfolg haben werden. Jedenfalls zweifeln wir sehr stark an der Größe h als universeller Naturkonstante. Schon aus folgenden Gründen ist die Existenz von h als universeller Naturkonstante sehr zweifelhaft: Sämtliche Naturvorgänge können in einem Maßsystem beschrieben werden, das mit 3 unabhängigen Dimensionen auskommt. Also müssen alle physikalischen Gesetze mit einem Maßsystem beschreibbar sein, das auf drei universellen Naturkonstanten als Elementareinheiten aufbaut. Wir haben aber vier so genannte universelle Naturkonstanten, also muss eine zuviel da sein:

An den ersten drei Größen ist man nicht so leicht geneigt, zu zweifeln, wohl aber an der Vierten, zumal da sie selbst uns in Form der Sommerfeld'schen Feinstrukturkonstante vorführt, dass sie nicht unabhängig von e₀ , und c ist.
Kurz und gut, wir versuchen die Berechnung von mit dem Biot-Savart-schen Gesetz, obwohl wir genau wissen, dass dies schon vom Ansatz her falsch ist und daß an irgendeiner Stelle Schiffbruch erlitten werden muss. Trotzdem wird das Wagnis durchgeführt, weil wir hoffen, doch solche Argumente zu finden, die uns weiterhelfen können.

XVII    

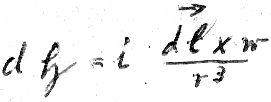
Da wir nun unseren Magnetfeldsatz aufgestellt haben, suchen wir nur in der Raumrichtung, die der Projektion der in der Abbildung 8 dargestellten Ellipse entspricht. (Die Zeichnung ist der Anschaulichkeit halber so ausgeführt, dass der Betrachter die Ellipse etwas geneigt sieht).

Für einen in einer Ebene bleibenden Stromfaden aber lässt sich das Biot-Savart-sche Gesetz etwas vereinfachen (Abb. 15).

  XVIII  

  XIX  

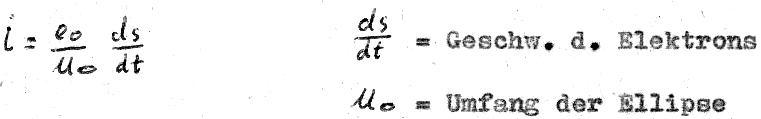
Wir wollen also genau auf dem Umfang der Ellipse berechnen, was sicher falsch ist. Trotzdem sei es gewagt:

  XX  

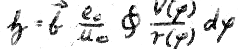
Wir vereinfachen etwas, da 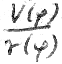auf der Ellipse schwierig anzugeben ist (Abb. 16).

  XXI  

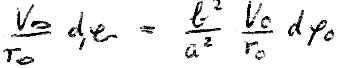
Diese Gleichung gilt, weil 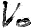und aus der Kippung eines mit konstanter Geschwindigkeit umlaufenen Kreises entstanden sind.
Daraus folgt:

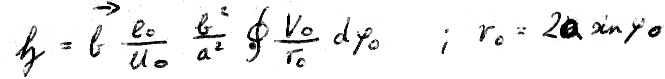
  XXII  

Und schon ist der Punkt erreicht, an dem die Rechnung nicht mehr weiter geführt werden kann, denn das ist gleich

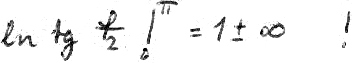
Ebenso macht uns die Binormale nun sehr zu schaffen, denn sie steht senkrecht auf unserer Zeichenebene und nicht - wie wir es brauchen - auf dem zweiten Kleinkreis, der ja gegen die Zeichenebene geneigt ist (Gleichung XXI beeinflusst die Richtung der Binormale nicht). Trotzdem rechnen wir nun mit falschen Werten weiter - nur, um aus unseren Fehlern zu lernen, denn sicherlich verbirgt sich hinter diesem n ein noch nicht erkanntes Prinzip, dessen Inhalt sich vielleicht schon teilweise durch die Fehler unserer Rechnung andeutet.

Wir drehen also die Binormale gewaltsam in die gewünschte Richtung und nennen das undefinierbare Integral: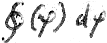
Daraus folgt:

  XXIII  

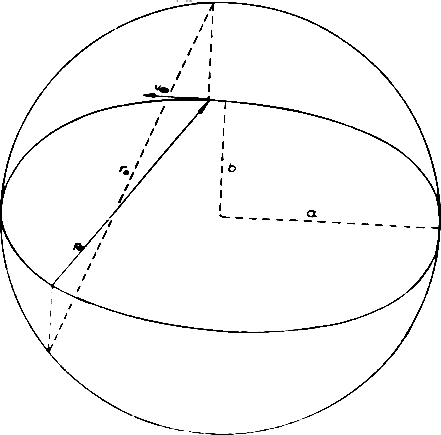
Nun setzen wir gleich der Zentrifugalkraft auf den Kleinkreisen:

  XXIV  

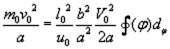
  XXV  

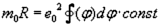
So, und nun wollen wir die Phantasie spielen lassen:

Wir vermuten, dass das 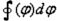mehrdeutige Lösungen enthält und dass es eine lineare Funktion von 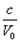ist, denn dann entsteht eine Quantenvorschrift:

  XXVI  

Das hieße, dass 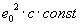gelten könnte! Errechnet man den Zahlenwert von 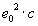, stellt man fest, dass dieser nur ca. 3 Zehnerpotenzen vom Wert des Planck'schen Wirkungsquantums entfernt ist Aber all diese Vermutungen sind eben auf Sand gebaut und wir wollen nun darangehen, die Fehler zu beseitigen und aus der Niederlage zu lernen.

Denn nun sind wir soweit gelangt, dass wir zum entscheidenden Satze kommen können:

Das Biot-Savart´sche Gesetz ist dafür geschaffen, aus irgendeiner stromdurchflossenen Leiterschleife ein Magnetfeld zu berechnen. Woran aber erkennt man dessen Stärke, Richtung usw.? Sicherlich daran, dass man die Wirkung dieses Magnetfeldes auf irgendeinen anderen Magneten oder mindestens eine Ladung e₀ misst. Da es aber bekanntlich gar keine Elementarmagneten gibt, gehören zur Erfüllung der Voraussetzungen für die Heranziehung des Biot-Savart´schen Gesetzes mindestens zwei Elektronen, nämlich eines, das das Feld erzeugt und ein zweites, dessen Veränderungen festgestellt werden müssen. Das Biot-Savart´sche Gesetz regelt also die Abhängigkeiten von mindestens zwei Elektronen untereinander (wie überhaupt fast alle Gesetze der Physik natürlich darauf abgestimmt sind, Ursache und Wirkung an verschiedenen Objekten zu untersuchen).

Wie aber sieht es aus, wenn Ursache und Wirkung an einem Objekt auftreten? Denn es ist doch durchaus nicht ausgeschlossen, dass ein Elektron auch einmal mit seinem eigenen Magnetfeld in Konflikt geraten kann (was ja in unserem Atommodell der Fall sein soll). Oder wollen wir etwa für diesen einen Fall die Existenz des Magnetfeldes leugnen?

Das können wir auf gar keinen Fall, denn wir kennen alle aus der makroskopischen Erfahrung den Begriff der Selbstinduktion. Dieser physikalische Effekt, der auf die - dem Magnetfeldsatz entsprechende - Bewegung einer Gruppe von Elektronen zutrifft, muss natürlich auch für ein einzelnes Teilchen gelten. Man kann sich diese Schlussfolgerung sofort herleiten, wenn man die Tatsache benutzt, dass bei einer Gruppe von Elektronen das einzelne Elektron nicht von den anderen unterschieden werden kann. Wir betrachten also ein einzelnes Elektron dieser Gruppe. Es erzeugt (wie alle anderen) das Magnetfeld. Nun wirkt ja bekanntlich das einmal erzeugte Teilmagnetfeld dieses einen Elektrons auf alle anderen Elektronen. Da aber die Elektronen nicht unterscheidbar sind, muss das „Teilmagnetfeld” auch auf seinen Erzeuger zurückwirken, was zu beweisen war.

Nun aber wollen wir noch einen Satz, den wir eben ausgesprochen haben, erweitern: Wie aber sieht es aus, wenn Ursache und Wirkung an einem Elektron auftreten und kontrolliert werden sollen? Selbstverständlich ist hier eine Kontrolle nicht mehr möglich, weil bei jedem Eingriff in diesen Mechanismus Veränderungen unausbleiblich wären. Das ist der wahre Inhalt der Heisenberg´schen Unschärferelation, die ja als "Eingriffsgrenze" das Planck´sche Wirkungsquantum vorgibt.

Also folgern wir:

1. Die Anwendung des Biot-Savart´schen Gesetzes musste scheitern, weil sie auf falschen Voraussetzungen aufbaute.
2. Das unbekannte Prinzip, das wir suchen, kann nur noch so lauten:

Aus diesem Grunde ist es erstens ein Wirkungs- und zweitens ein Quantum, und aus eben diesem Grunde kann man Quantengesetze nicht „er-messen”, sondern man muss sie erraten!

Übrigens versagt aus genau diesem Grunde auch die Anwendung der Formel über die Lorentz-Kraft. Ja, es ist von nun an in jedem Falle geboten, alle mathematischen Formulierungen und physikalischen Vorstellungen genauestens zu überprüfen, ob sie anwendbar sind.

Zunächst wollen wir die Begriffe „eigene Wechselwirkung” und „fremde Wechselwirkung” einführen, natürlich im Sinne des oben formulierten Satzes.

Weiterhin schauen wir uns nach Ansatzpunkten für eine mathematische Behandlung der gestellten Aufgabe um. Das ist nun zunächst ziemlich entmutigend, da ja alle Quanteneffekte Wahrscheinlichkeitscharakter tragen - übrigens in vollkommener Harmonie mit unserer Vorstellung, denn jeder physikalische Wechselwirkungsmechanismus eines Teilchens kann sich in zwei Richtungen entfalten: Entweder das Teilchen tritt mit sich selbst in Wechselwirkung - oder es tritt mit anderen Teilchen in Wechselwirkung. Und hier liegt auch der Grund für den Dualismus dar Materie: Bei fremder Wechselwirkung haben wir klassische Physik - bei eigener Wechselwirkung - Quantenphysik. Will man aber alles vom Standpunkt der klassischen Vorstellung (der fremden Wechselwirkung) her verstehen, dann erhebt sich als unüberwindliche Schranke eine Unschärferelation, die genau durch die Größe der Wechselwirkungskonstante der eigenen Wechselwirkung einer Ladung vorgegeben ist.

Betrachtet man unter diesem Aspekt der eigenen - bzw. fremden Wechselwirkung die bis jetzt erzielten erfolgreichen Deutungen, die durch das Modell erzielt wurden, dann erscheinen sie nun in einem viel besseren, hellerem Licht. Das „Versteckspiel” beim Pauli-Prinzip z.B. kann nun nur so gedeutet werden, dass durch diese Bahnanordnung die eigene Wechselwirkung ungestört ablaufen kann. Ebenso verstehen wir nun das „Ausweichen” beim Stern-Gerlach-Effekt.

Doch wir schweifen ab von unserer Aufgabe - der Berechnung des Planck´schen Wirkungsquantums. Wir suchen also einen Quanteneffekt, der uns gestattet, mathematische Gesetze der eigenen Wechselwirkung zu finden. Da wir keine Mischung zwischen klassischer und Quantenphysik wünschen, die uns nur die Hälfte der Wahrheit angeben kann (die andere Hälfte entfällt auf den mit endlicher Wahrscheinlichkeit existierenden Teil der klassischen Physik, der für uns uninteressant ist), suchen wir also einen Quanteneffekt, der mit Sicherheit - nicht mit Wahrscheinlichkeit - eintritt. Außerdem muss dieser Quanteneffekt sich durch völlige Reibungsfreiheit auszeichnen - denn wie will ein Teilchen sich an sich selbst reiben? Zum dritten fordern wir - eben wegen der Reibungsfreiheit - dass der Energieerhaltungssatz für diesen Vorgang gelten soll. Wir suchen also eine Art bescheidenes Perpetuum mobile, das unbegrenzt in Bewegung bleibt - ohne allerdings Energie zu erzeugen oder zu vernichten.

Das ist natürlich die Supraleitung. Wir werden also die Zusatz-Gleichungen zu den Maxwell-Gleichungen, die v. Laue und London auf phänomenologischem Wege gefunden haben und denen der Suprastrom genügen soll, verwenden und deuten sie so: Bei der Supraleitung haben wir den Fall, dass ein äußeres Magnetfeld in den Richtungen 1, 2, 3 oder 4 unseres Modells antiparallele Ausrichtung erzeugt. Diese Annahme bedarf nun aber einer etwas ausführlicheren Erklärung:

Es ist ja bekannt, dass es mehrere Arten von Magnetismus der Materie gibt. Den Ferromagnetismus deuten wir - ebenso wie die Quantentheorie - als einen zum äußeren Magnetfeld ausgerichteten Spinmagnetismus - natürlich im Sinne des eingeführten "Bahnspin". Dieser Magnetismus ist in jedem Falle der Teil des Magnetfeldes unserer Bahn, der nach außen wirksam wird. Er entspricht also der fremden Wechselwirkung und verhält sich demnach klassisch, richtet sich also in äußeren Feldern nach diesen aus und erscheint - wenn keine ihn ordnenden Gittervorschriften existieren - als Paramagnetismus. Den Diamagnetismus dagegen müssen wir der eigenen Wechselwirkung zuschreiben. Durch die Erklärungen, die wir bei der Richtungsquantelung und beim Pauli-Prinzip abgaben, sind wir gezwungen, festzustellen, dass die eigene Wechselwirkung - sofern sie nicht „vernichtet werden will”. - in jedem Falle das Bestreben hat, äußeren Feldern auszuweichen, oder - wenn das nicht möglich ist - ein Gegenfeld aufzubauen. Da aber der Supraleiter ideal diamagnetisch ist und außerdem die von uns geforderten Bedingungen der Reibungsfreiheit usw. erfüllt, ist zu erwarten, dass die Gleichungen, denen der Suprastrom genügt, tatsächlich die Gleichungen sind, die die eigene Wechselwirkung regieren. Allerdings müssen wir nun fordern, dass bei den Elektronen, die den Suprastrom erzeugen, keinerlei fremde Wechselwirkung vorliegen darf, dass also für diese Elektronen gelten muss, dass ihre Spinmomente paarweise abgesättigt sind. Diese Forderung, die mit der von der Quantentheorie gegebenen Erklärung der Supraleitung übereinstimmt, wird ebenfalls als ein Indiz für die Richtigkeit unseres Modells gewertet. Weiterhin erkennen wir, dass bei Spinabsättigung unseres Modells - also bei Vollbesetzung der „Kugelschale” die beiden Elektronen tatsächlich um eine der vorgegebenen Raumrichtungen (z.B. Richtung 1) den gleichen Umlaufssinn haben. Das heißt, dass bei Spinabsättigung (keine fremde Wechselwirkung) die Felder der eigenen Wechselwirkung sich nicht gegenseitig aufheben, also durchaus Diamagnetismus vorliegen kann.

Wir deuten also die beiden Zusatzgleichungen, die London und v. Laue gefunden haben, als Gleichungen der eigenen Wechselwirkung und geben nun den folgenden Weg, den wir beschreiten werden, in groben Zügen an: Vorausgeschickt sei nur, dass der bisher beschrittene unfruchtbare Weg nun nicht wieder beschritten werden darf - denn nach den bisher formulierten Sätzen ist es nun sinnlos, von Lorentz-Kraft und Zentrifugalkraft im bisher üblichen Sinne zu sprechen.

Aus eben diesem Grunde müssen wir einen völlig anderen Weg einschlagen, der den formulierten Forderungen entspricht. Wir werden also mit Hilfe der beiden o.a. Gleichungen für und versuchen, den Energieerhaltungssatz - der ja weiterhin gelten soll - anzuwenden und mit diesen Mitteln h berechnen.

Der aufmerksame Leser wird bemerkt haben, dass bei den bisherigen Rechnungen keine einheitliche Linie bezüglich des verwendeten Maßsystems bestand. Wir entscheiden uns nun und verwenden das Gauß´sche CGS-System und schreiben die beiden Gleichungen für und zunächst erst einmal auf:

  XXVII  

  XXVIII  

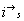  ist der Suprastrom, ns ist die Konzentration der an der Supraleitung beteiligten Elektronen. Zunächst besteht für uns die Aufgabe, diese beiden Gleichungen für ein Elektron umzuschreiben. Dabei verfahren wir für die Größe 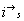in der üblichen Weise:

  XXVIX  

Wir betrachten also - wie vereinbart - unsere Raumkurve aus der Sicht der Richtung 1 z.B. und wählen für den Weg, den das Elektron beschreitet, die gesamte Strecke, die das Elektron bei einem Umlauf auf eine Projektion senkrecht zur Richtung 1 entwirft. Diese Größe bezeichnen wir als 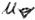. Nun wenden wir uns der Größe n_s zu:

ns  =	Anzahl der an der Supraleitung beteiligten Elektronen	=	n
	Sekunde		sek.

Die Sekunde schreiben wir ebenfalls um (wir begehen keinen allzu großen Fehler, wenn wir nur ganze Umlaufzahlen zulassen):
1 Sekunde ≈ Anzahl der Umlaufszeiten * Umlaufszeit

  XXX  

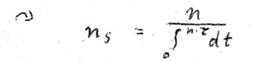
Nun, da wir nicht geneigt sind, über viele Elektronen zu summieren, nehmen wir eine andere Auffassung zu Hilfe, die uns gestattet, n_s für ein Elektron auszudrücken. Dazu sei folgendes Beispiel gegeben: Wenn 6 Elektronen in der Sekunde je einen Umlauf vollführen, gilt für .

Das gleiche Ergebnis erhält man, wenn man ein Elektron sechsmal schneller umlaufen lässt:

Damit haben wir erreicht, was wir wollen: Wir fassen die Zahl n als eine Zahl von Umläufen auf, die ein Elektron in einem festen Zeitraum ausführen kann und fordern nun, dass diese Zahl eine ganze Zahl sein soll. Diese Forderung begründen wir damit, dass unser Magnetfeldsatz verbietet, ein magnetisches Feld überhaupt als existent zu diskutieren, wenn nicht mindestens ein ganzer Umlauf vorliegt. Damit haben wir anschaulich eine Hauptquantenzahl n eingeführt.

Wir schreiben also:

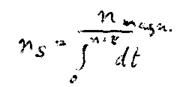
Das müsste nun also für magnetische Felder gelten.

Ähnlich verfahren wir mit dem n_s, das in der Gleichung des elektrischen Feldes steht; doch dazu müssen wir etwas weiter ausholen:

Wir hatten ganz am Anfang gefordert, dass am Kern bei dem Einhalten unserer Modellbahn „magnetische Windstille” herrschen soll. Daraus hatten wir abgeleitet, dass diese Bahn strahlungslos sein muss, denn zur Energieabgabe (Abstrahlung von Lichtquanten) braucht man ein elektrisches und ein magnetisches Feld. Ebenso folgern wir nun: Wenn nur bei einem vollen Umlauf ein magnetisches Feld existiert, dann ist für die Angabe einer Energie auch nur dann das elektrische Feld existent, wenn existiert. Das heißt, dass ebenfalls für das elektrische Feld nur ganze Zahlen n in frage kommen, denn wir wollen ja den Energieerhaltungssatz anwenden. Wir verallgemeinern also:

Dieser wichtige Satz lässt uns aufhorchen, denn wir kennen eigentlich solche Energiepakete in Gestalt der Lichtquanten. Das heißt, dass die Lichtquanten (die elektromagnetischen Wellen) solche Gebilde der eigenen Wechselwirkung sind. Damit zerfließt also der Streit um die Zuordnung von Wellenpaketen, die nun den Teilchen in Gestalt der de-Broglie-Wellen zuschreiben kann, in ein Nichts: Ebenso, wie die Lichtquanten Produkte der eigenen Wechselwirkung sind, haben die Teilchen (zunächst die geladenen Teilchen) ebenfalls die Eigenschaft, eigene Wechselwirkung zu zeigen - mit der Maßgabe, dass hier nur Kombinationen von und zulässig sind - sie haben also Wellencharakter. Sie besitzen mit anderen Worten die Fähigkeit, mit sich selbst in Wechselwirkung zu treten.

Doch nun zurück zu unserer - beim -Feld zu wählenden Quantenzahl. Wir dürfen diese - nach dem bisher Gesagten nicht gleich n magn. wählen, denn wir haben ja gefordert, dass nur dann eigene Wechselwirkung zustande kommen kann, wenn das Elektron bereits einen Umlauf absolviert hat, also ein magnetisches Feld bereits vorhanden ist. Daraus folgt:

n _elektr. = n _magn. + 1

Nun können wir also für die Gleichungen XXVII und XXVIII schreiben:

  XXXI  

  XXXII  

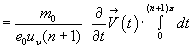
Aber selbst mit diesen Gleichungen sind wir nicht zufrieden, denn vor den Integralen stehen Funktionen der Zeit (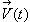). Für die Summation über viele Elektronen (bei der Supraleitung) ist diese Schreibweise sicher richtig, falsch ist sie aber bei einem Elektron. Wir müssen also, wenn das Teilchen mit sich selbst in Wechselwirkung treten soll, fordern, dass alle von t abhängigen Größen unter die Integrale gehören. Dabei heben sich beim -Feld die Differentiation und die Integration über t auf, weil V auf der Ellipse nur von t abhängt, also partielles und totales Differential nach der Zeit gleich sind. Diese Schreibweise ist kein Willkürakt, denn bei der Betrachtung vieler Elektronen ist sicherlich eine Funktion des Ortes im supraleitendem Material. (Das Innere des Suprakristalls ist ja bekanntlich durch den an der Oberfläche fließenden „Suprastrom” abgeschirmt.)

Wir betrachten also ein an der Oberfläche des Kristalls befindliches Elektron:



  XXXIII  
=

  XXXIV  

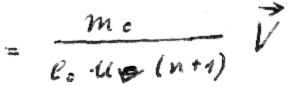
Betrachtet man nun diese beiden Gleichungen und denkt daran, dass bei der Errechnung der Energie - die wir ja an irgendeiner Stelle unserer Rechnung angeben wollen - das Produkt von und auftauchen muss, so würde bei diesem Produkt im Nenner die Größe n (n + 1) erscheinen! Das ist vielleicht die Ursache dafür, dass in der Quantentheorie für das Quadrat des Drehimpulses die Größe stehen muss! Ihre anschauliche Deutung haben wir eigentlich schon gegeben: Eigene Wechselwirkung ist nur dann möglich, wenn bereits ein Umlauf absolviert wurde (wegen des Magnetfeldsatzes). Wir werten diese kleine Zahlenspielerei wiederum als Indiz für die Richtigkeit unseres Weges und gehen nun an die Berechnung des Magnetfeldes nach Gleichung XXXIII. Mit Befriedigung registrieren wir, dass diesem Magnetfeld nicht der Nachteil der Unmöglichkeit der zu erwartenden Ergebnisse anhaftet - wie dem Biot-Savart´schen Gesetz.

Noch eine kleine Korrektur in dieser Gleichung ist notwendig - diese begründen wir in üblicher Weise mit dem Magnetfeldsatz: Unter τ werden wir nun im folgenden nicht mehr die ganze Zeit verstehen, die das Elektron benötigt, um seine „Taumelbahn” abzulaufen, sondern nur die Umlaufszeit für die in Richtung 1 sichtbare Ellipse, denn außerhalb dieser stetigen und in der räumlichen Ableitung stetigen Raumkurve ist ja kein Magnetfeld vorhanden! Ebenso argumentieren wir, wenn wir nur für diese Ellipse errechnen und die übrigen Teile der Bahn nicht betrachten.

Also schreiben wir:

  XXXV  

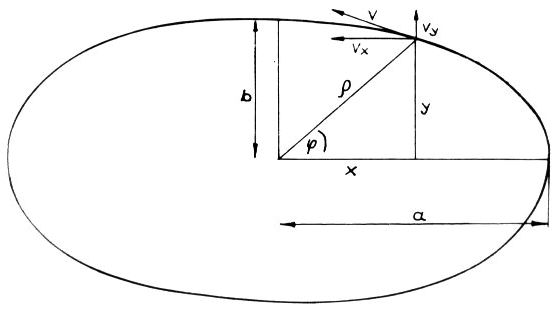
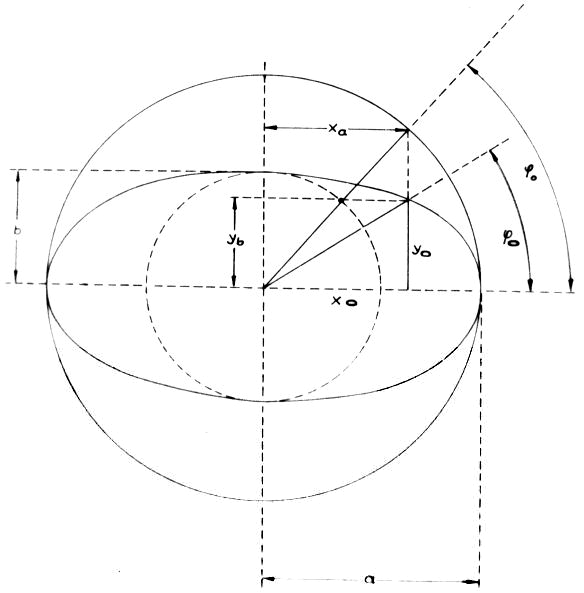
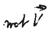in kartesischen Koordinaten (Abb. 17)

Daraus folgt:

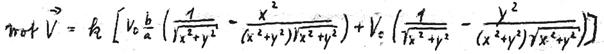
a ist der Radius des Kleinkreises:
b aus den Größen des Oktaeders:

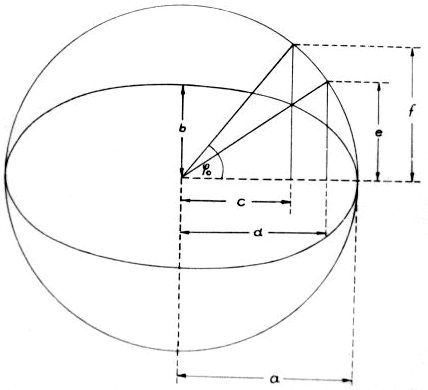
Wir schreiben nun 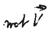in Zylinderkoordinaten, indem wir folgende Größen einführen (Abb. 18):

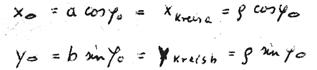
Wir bevorzugen diese Gröen, weil sie uns das Integrieren ganz erhebllich erleichtern:

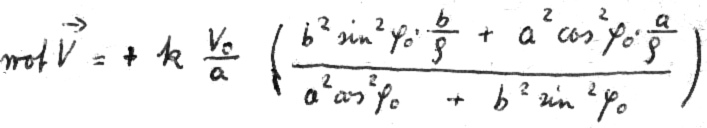
und

Daraus folgt: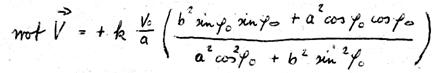


Da wir gern alle Größen durch Größen der Kreise ausdrücken wollen (was - wie gesagt - das Integrieren erheblich erleichtert), führen wir noch folgende Größen ein (Abb. 19):

Daraus folgt:

Den Ausdruck, der auf der rechten Seite in der Klammer steht, nennen wir S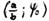. Diese Funktion S 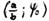ist stetig über 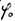und besitzt keine Unstetigkeitsstellen bezüglich ihrer Ableitung nach 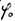. Sie ist allerdings nicht mehr elementar ausdrückbar. Jedoch lässt sie sich sehr bequem graphisch erzeugen, wenn man die Ellipse und den dazugehörigen umbeschriebenen Kreis aufzeichnet und die in der Abbildung 20 angegebenen Strecken ausmisst.

  XXXVI  

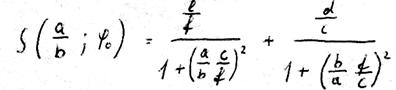
Für unseren Fall der Größen a und b ist sie eine wenig von 1 verschiedene Größe, die sinusähnlich verläuft.

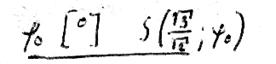0	1,0
10	1,0024
20	1,0065
30	1,097
40	1,0130
50	1,0270
60	1,0130
70	1,0085
80	1,004
90	1,0

Diese Funktion kann man nun recht mühelos graphisch integrieren und erhält:

  XXXVII  

Daraus folgt für :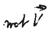

Nun, da alle Größen auf den Kreis zurückgeführt sind. können wir berechnen:

  XXXVIII  

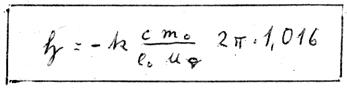
Zwei interessante Ergebnisse wollen wir zunächst nur registrieren: Erstens erscheint das -Feld ohne Quantenzahl, denn diese kürzt sich nach der Integration heraus. Ebenfalls stehen in dieser Gleichung nun außer nur noch Konstanten. Das ist die mathematische Formulierung unseres Magnetfeldsatzes. Ein Elektron kann bei irgendeinem Umlauf nur ein Magnetfeld erzeugen, dessen Stärke im Wesentlichen nur von dem Weg, den das Elektron abläuft, abhängt. Dabei darf nur der Teil des Weges zur Erzeugung des -Feldes beitragen, der eine stetige und in der räumlichen Ableitung stetige geschlossene Raumkurve umschließt

Wir haben also nur deshalb Quantenvorschriften weil kein kontinuierliches Spektrum von Elementarladungsstärken existiert. Die Wurzel aller Quantenvorschriften ist also die Tatsache, dass wir nur eine Elementarladungsstärke in der Natur finden. Thus, we only have quantum rules because there is no continuous spectrum of elementary charges. Consequently, the root of all quantum rules lies in the fact that we find only one specific elementary charge in nature.

Zum zweiten nehmen wir die eigentümliche Tatsache zur Kenntnis, dass das -Feld von der Größe des Verhältnisses (was ja in der S-Funktion enthalten ist) abhängt. Wenn wir uns jetzt einmal - abgesehen von unserem speziellen Beispiel - irgendeine andere Ellipse ausdenken, deren Hauptachsenverhältnis bedeutend größer als das gegebene sei, dann müssen wir feststellen, dass das Magnetfeld zugenommen hat. Das hieße, dass das Magnetfeld bei eigener Wechselwirkung immer größer wird, je starker die Neigung eines umlaufenen Kreises wird, wenn er unter verschiedenen Neigungswinkeln betrachtet wird. Dieses - mit der klassischen Erfahrung durchaus nicht vereinbare Resultat - wollen wir zunächst so stehen lassen, um bei gegebenem Anlass darauf zurückzukommen.

Nun schreiten wir zur Berechnung der Energie des Teilchens. Dazu benutzen wir die Gleichungen für und

Da wir schon gesagt hatten, dass die Angabe einer Energie nur dann sinnvoll ist, wenn existiert - also der Magnetfeldsatz erfüllt ist -, müssen wir nun , so angeben, dass nur die Komponente von zur Rechnung herangezogen wird, die in Richtung 1 zu erkennen ist. Das heißt, dass das 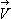in der Gleichung für durch ersetzt werden muss:

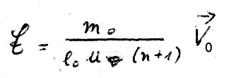
Nun stehen also und in jedem Falle senkrecht aufeinander und die Schwierigkeiten, die uns einst die Binormale bereitete, sind fast beseitigt. Das „Fast” müssen wir noch erläutern: hat ein negatives Vorzeichen, was uns bei der Produktbildung von und zwangsläufig zu der unsinnigen Lösung einer negativen Energie führen würde. Wir hatten aber schon bei unseren Erklärungsversuchen der Richtungsquantelung des Diamagnetismus und der Supraleitung bereits festgestellt, dass die eigene Wechselwirkung - sofern sie nicht vernichtet werden will - entweder äußeren Feldern ausweicht - oder, wenn das nicht möglich ist, ein Gegenfeld aufbaut. Da wir aber unsere -Gleichung aus der Supraleitung entnommen haben, wo äußere Felder gemessen werden, dürfen wir nun für die eigene Wechselwirkung ohne große Skrupel das Vorzeichen von umkehren:

  XXXIX  

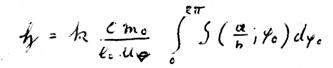
Wir schreiben nun noch einmal dazu:

  XL  

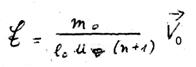
Beiden Gleichungen haftet ein Nachteil an. Beim -Feld haben wir diesen bereits über die Funktion diskutiert. Beim -Feld entsteht er durch folgenden Umstand: Wir haben uns vorgenommen, die eigene Wechselwirkungsenergie eines Teilchens zu berechnen, die letztendlich aus einem Produkt von und berechnet werden soll. Diese eigene Wechselwirkungsenergie soll eine Konstante sein, denn wir haben ja festgestellt, dass ein Teilchen nur mit der Größe eines Wechselwirkungsenergiequantums mit sich selbst in Wechselwirkung treten kann. Dieses Quantum sollte irgendwie mit dem Planck´schen Wirkungsquantum zusammenhängen, so dass man h berechnen kann. Nun kommen wir zu dem erwähnten Nachteil, der anhaftet: ist keine Konstante, weil variabel ist. Dadurch - so könnte man sagen - kann man auch kein Wechselwirkungsenergiequantum für die Energie erhalten. Dieser Widerspruch - ebenso wie der Widerspruch der im -Feld steckt - löst sich ganz einfach, wenn wir nur die bisher aufgestellten Aussagen konsequent anwenden: Es gibt bei eigener Wechselwirkung keine reine magnetische Energie - ebenso wie es keine reine elektrische Energie geben kann.

Unsere beiden Widersprüche sind aber aus der klassischen Vorstellung über und entstanden und wir haben noch gar kein Recht, ein abwertendes Urteil zu fällen, bevor wir nicht diese eigene Wechselwirkungsenergie berechnet haben. Wir betrachten also und als leicht verzerrte Abbilder eines Bildes der Natur, das wir zurzeit eben noch unscharf erkennen können, weil die Hilfsmittel (,), mit deren Hilfe wir betrachten wollen, uns einfach nicht gestatten, schärfer sehen zu können. Allein die Kombination von und - also die eigene Wechselwirkungsenergie - wird es uns gestatten, schärfer sehen zu können, denn diese ist im Bereich der eigenen Wechselwirkung existent.

Wir wiederholen diesen Gedanken noch einmal ausdrücklich, denn er ist äußerst interessant: Im Bereich der eigenen Wechselwirkung existiert nur das Produkt von und , also eine Energie - über alle anderen Energieformen - wie z.B. reine elektrische, bzw. reine magnetische Energie - zu diskutieren ist müßig, weil beide nicht vorhanden sind. Aus diesem Grunde also erhält auch die Quantentheorie Aussagen über Energien, Energieniveaus, Energiequanten, Energiesprünge usw. Wir bemerken dies, weil wir diese Aussage - die letztendlich auf unseren eingangs formulierten Magnetfeldsatz zurückgeführt werden kann - wiederum als ein wichtiges Indiz für unsere Vorstellung registrieren.

Zur Berechnung der Eigenwechselwirkungsenergie wollen wir die Gleichung benutzen, die zur Herleitung des Poynting'schen Vektors für Lichtquanten führt. Wir erwarten, dass diese Gleichung ohne weiteres auf das zu lösende Problem angewandt werden kann, da die Lichtquanten ja - nach unserer Vorstellung - Gebilde eigener Wechselwirkung sind.

  XLI  

Das Differential der Energie, das durch die Fläche F (die senkrecht auf der Ausbreitungsrichtung der Lichtwelle steht) strömt, ist gleich der durch 4π geteilten Länge des auf der Fläche F senkrecht stehenden Parallelepipeds, multipliziert mit den Absolutwerten von und , die in der Ebene der Fläche F liegen. Dabei ist die Länge des Parallelepipeds gegeben durch die im Zeitraum dt abgelaufene Strecke des Lichtstrahles der Geschwindigkeit c. Selbstverständlich müssen wir diese Gleichung - die (gleich den Gleichungen der Supraleitung) summarischen Charakter trägt - für unser Elektron, also ein Teilchen umschreiben. Dabei sind wiederum Willkürakte vonnöten, wir hoffen, dass der Erfolg die unzulässigen Mittel rechtfertigt

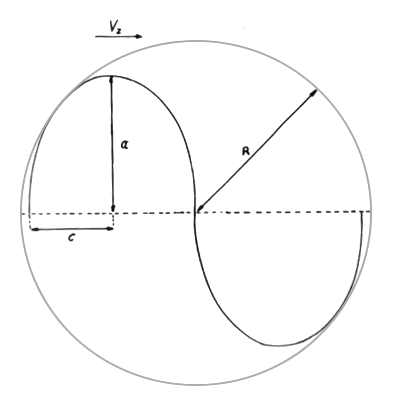
Als erstes ersetzen wir die Geschwindigkeit des Lichtes in Ausbreitungsrichtung der Welle durch die Geschwindigkeit des Teilchens in Richtung 1. Wir nennen diese Komponente Vz. Wir blicken also nun in Richtung b-d und zeichnen nur den Teil der Bahn. der zur Erzeugung einer in Richtung 1 sichtbaren geschlossenen Ellipse notwendig ist (Abb. 21):

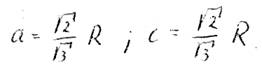
Daraus folgt für Vz:

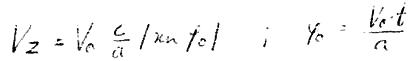
Diese Gleichung ist eine Näherung für Vz. Exakt müsste auch hier wieder eine elliptische Funktion stehen, die aber nicht stark von der vorgeschlagenen Näherung abweicht.

Wir schreiben also nun für die Gleichung; des Poynting-Vektors:

  XLII  

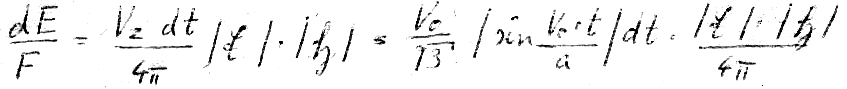
Und nach Integration über 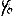von 0 bis 2π (wegen des Magnetfeldsatzes):

  XLIII  

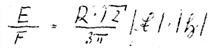
Wir haben nun die Energie. die durch die Fläche F strömen würde, wenn nur diese Ellipse andauernd ablaufen würde. Das ist aber nicht der Fall, denn bei unserem Modell gibt es durchaus Zeitpunkte, in denen wir keine Energie in der Richtung 1 finden, nämlich dann, wenn das Elektron die Teile der Bahn abläuft, die keinen Beitrag zur Energie liefern sollen.

Dieser in Gleichung XLIII angegebene Betrag der Energie ist nur bei einem Achtel des vollen Umlaufes des Elektrons um den Kern vorhanden. Ebenfalls ist dieses Achtel nur eine Näherung. Bei genauer Berechnung müsste man die Integrationsgrenzen in Gleichung XLII stetig ändern und dann mitteln. Da aber bei unserem Modell dieser Fehler nur klein sein kann (alle Ellipsen sind nicht stark „elliptisch”) begnügen wir uns mit dem Achtel.

Nun wird aber beim Poynting-Vektor gerade die Energie berechnet, die pro Zeiteinheit (z.B. Sekunde) durch die Fläche F strömt. Also müssen wir nun auch unsere rechte Seite der Gleichung, durch 8 teilen:

Nun kommen wir zum Einsetzen von und und schreiben der Übersichtlichkeit halber noch einmal Gleichung XXXIX und XL auf:

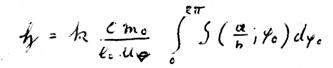
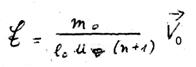
Auf jeden Fall sind nun bei beiden Größen Schönheitsfehler zu entdecken. Wir diskutieren zuerst den Schönheitsfehler von , den wir schon weiter oben angedeutet haben: ist keine Konstante - wir fordern aber für unseren Fall E = const!, weil wir - entsprechend unseren Erwartungen über ein Eigenwechselwirkungsquantum E = const. setzen müssen, denn wir wollen ja den Energieerhaltungssatz auch im Bereich der eigenen Wechselwirkung gelten lassen. Zum zweiten müssen wir E = const. setzen, wenn wir dem bescheidenen Perpetuum mobile der Supraleitung Rechnung tragen wollen.

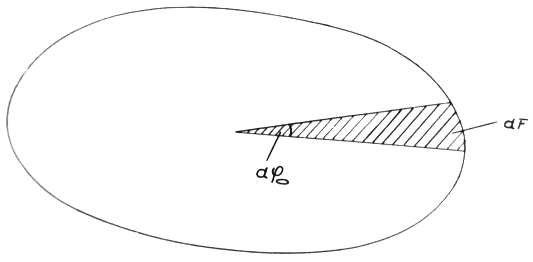
Wir schreiben deshalb für die Fläche F (die wir selbstverständlich mit der Fläche der Ellipse in Richtung 1 identifizieren) unsere bewährte Integralform und verfahren in der gleichen Weise mit diesen Größen wie bei der Behandlung von n_s:

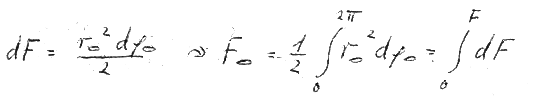
(Abb. 22)

Da aber V₀ eine Variable von 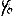ist, gehört sie - bei eigener Wechselwirkung eines Teilchens mit sich selbst - unter das Integral - und die Schwierigkeit der Variabilität von V₀ und damit von E ist überwunden:

  XLIV  

Wir drücken nun in üblicher Weise die elliptischen Funktionen durch Größen der Kreise aus:

  XLV  

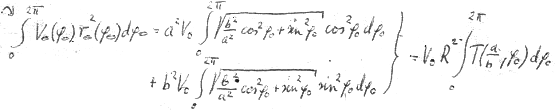
T ist nun ebenfalls eine nicht mehr elementar integrierbare elliptische Funktion
- genau wie S. Man kann sie aber ebenfalls recht bequem graphisch integrieren. In unserem Fall der Größen a und b erhält das Integral die Größe 0,50077 * 2π Es ist also eine - wenig von π verschiedene Größe.

Daraus folgt:

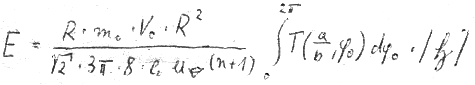
Nun kommen wir zu dem schon erwähnten Schönheitsfehler von :
Es existiert keine Komponente von in der Ebene der Fläche F, sondern steht auf dieser Fläche senkrecht. Der Poyntingvektor ist aber für Energieströmungen gültig, bei denen und eine Komponente in der Ebene der Fläche F haben. Nun, wir nehmen diese Eigenart der „Teilchenwelle” zunächst zur Kenntnis und rechnen mit der Komponente von weiter, die uns zur Verfügung steht. Wir sind sonst nämlich gezwungen, den Magnetfeldsatz als falsch zu bezeichnen - und gerade dieser hat uns eine Serie von schönen Indizien für die Richtigkeit unseres Weges beschert. Andererseits sehen wir auch kein Argument, dass man unbedingt bei einem geladenen Teilchen genau die gleichen Vorschriften zu erwarten hat wie bei Photonen, denn noch wissen wir zu wenig über die Mechanismen, die nicht mehr streng herleitbar sind und - wir sagten es einleitend - gewisse Willküren sind bei unserer Verfahrensweise unvermeidbar.

Wir schreiben also:

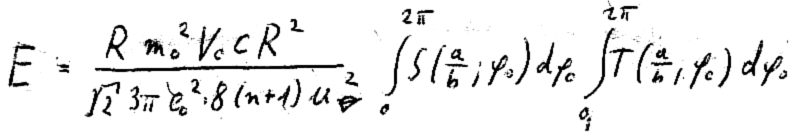
Nun wird es hochinteressant:
Da wir nach Abb. 4 vier solcher Eigenwechselwirkungsmechanismen in Gestalt der vier eingezeichneten Richtungen 1, 2, 3, 4 entdeckt haben, ist E also ein Viertel der Eigenwechselwirkungsenergie, die ein Elektron auf seiner vollständigen Taumelbahn entfalten kann. Daraus folgt:

  XLVI  
const. = E total = 4 ⋅ E =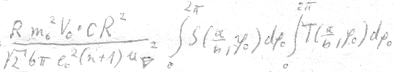

Wir fordern - wie schon oft angekündigt, dass E ges. = const. sein soll. Außerdem ist 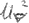von der Dimension R². Das heißt, dass in dieser Gleichung die Bohr´sche Drehimpulsquantelungsvorschrift enthalten ist:

  XLVII  
const. = E total = 4 ⋅ E =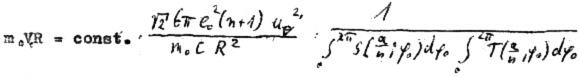

denn auf der rechten Seite stehen (abgesehen von der geringfügigen Variabilität des m ≈ m₀) nur noch Konstanten.



Doch nun wenden wir uns der Konstante zu:
Da die Supraleitung in unmittelbarer Nähe des absoluten Nullpunktes auftritt, sagen wir nun: Die für die Supraleitung verantwortlichen Elektronen nehmen bereits kurz vor Erreichen des absoluten Nullpunktes die kleinste Energieform an, die überhaupt ein Elektron annehmen kann, sie sind schon kurz vor den Nullpunkt „eingefroren”. Sie haben jede Art von fremder Wechselwirkung eingebüßt (wie wir bereits durch die paarweise Spinabsättigung forderten) und damit ist ihre gesamte Eigenwechselwirkungsenergie die einzige, die sie besitzen. Diese Eigenwechselwirkungsenergie muss also gleich der kleinstmöglichen Energie eines Elektrons, also gleich der Ruheenergie sein:

  XLVIII  
const. = m₀c²

Daraus folgt mit guter Näherung, weil hier m = m₀ gesetzt wird:

  XLIX  
m₀V₀R=

Die im umrandeten Feld stehende Konstante müsste nun den Zahlenwert des Planck´schen Wirkungsquantums ergeben und wir überprüfen:

Dagegen ist der experimentell gefundene Wert von h:

h = 6,625 * 10^-27 erg sek

Das ergibt eine Übereinstimmung mit dem von der Natur vorgegebenen Wirkungsquantum bis auf eine Differenz von ca. drei Prozent. Die erhaltene Abweichung führen wir auf die Näherungen zurück. Mit diesem Ergebnis ist zunächst das Ziel erreicht, obwohl noch viele Fragen von der kausalen Betrachtungsweise der Elementarvorgänge zu beantworten sind. Wir stellen aber fest, dass diese Übereinstimmung mit der von der Natur vorgegebenen Konstante h kein Zufall ist, denn der bisher dargelegte Weg entbehrt - trotz der Willkürakte - nicht einer gewissen Logik.

Bisher haben wir - bis auf wenige Ausnahmen - Indizien gesammelt, die die Richtigkeit unserer Betrachtungen bestätigen sollen. Die Berechnung des Planck´schen Wirkungsquantums dagegen fassen wir nun als ersten Beweis für die Richtigkeit unserer Hypothese auf. Das Planck´sche Wirkungsquantum ist also keine universelle Naturkonstante, wenn es einen Fall gibt, für den man es berechnen kann. Damit ist nun auch entschieden, warum alle Quantentheorien nur teilweise richtige Ergebnisse liefern: Sie gehen sämtlich von der Existenz dieses Quantums als universeller Naturkonstante aus und müssen dann alle Schwierigkeiten, die diese Voraussetzung in sich birgt, mit Unanschaulichkeit, Undeterminiertheit und künstlichen Modellen wie Spin, Dualismus usw. erkaufen. Mit dem Planck´schen Wirkungsquantum als universeller Naturkonstante stehen und fallen demnach alle Theorien über die Elenenterteilchen. Das erhaltene Ergebnis ist nun von ungeheurer Tragweite und man weiß zunächst gar nicht, womit man beginnen soll. Vielleicht ist es am besten, mit einer anschaulichen Vorstellung über den Mechanismus der eigenen Wechselwirkung zu beginnen. Wir lassen also das Elektron auf einer Bahn, die dem Magnetfeldsatz in irgendeiner Raumrichtung genügt, umlaufen. Dabei schneidet die Bahn laufend Feldlinien. Da aber die Bahn selbst auch eine Feldlinie sein muss, würden sich hier laufend Feldlinien schneiden. Wir wissen aber, dass es in der Natur keine - sich schneidenden Feldlinien geben darf. Dadurch wird ein Teil der Feldlinien laufend nach der konvexen Seite der Bahn gedrängt und wir erhalten bei einem stetig geschlossenen Kurvenzug einen Raumwirbel, wenn das Elektron seinen Umlauf beendet hat. Dieser Wirbel ist das Magnetfeld.

Wir wissen nun, dass außer der erratenen Bahn des Elektrons noch weitere Bahnen existieren, die bisher als Ellipsen bekannt sind. Nach unserer Vorstellung ergeben sich diese Bahnkurven natürlich als Taumelkurven auf Rotationsellipsoiden, wie in der Abb. 23 dargestellt. Auf solchen Rotationsellipsoiden werden die vier Kleinkreise zu Ellipsen verzerrt, der Oktaeder ist nun gestreckt und die vier Raumrichtungen, in denen eigene Wechselwirkung beobachtet werden kann, haben sich aufgerichtet. Weiterhin erkennen wir in Richtung e - f wiederum die Spinrosette. Ebenfalls ist auf dieser Bahnkurve das Produkt m * V * R = const., wenn wir den Kern in einen Brennpunkt des Ellipsoides setzen. Ebenfalls herrscht - wie bei dem kugelsymmetrischen Modell am Kern „magnetische Windstille”. Wir betrachten also - für den einfachsten Fall - ein Elektron, das den Wasserstoffkern auf einer solchen Bahn umläuft und wollen nun zeigen, dass das Verhältnis der beiden Achsen des Ellipsoides den Vorschriften der magnetischen und der Nebenquantenzahl entspricht, die die Quantentheorie fordert. Nur wenn das gelingt, ist gezeigt worden, dass h tatsächlich auf allen möglichen Bahnen, die den Kern umlaufen, eine Konstante ist. Wir haben also nachzuweisen, dass nur dann eine solche elliptische Bahn die Planck´sche Konstante erzeugt, wenn die in unserer Eigenwechselwirkungsgleichung vorkommenden elliptischen Integrale die richtigen Halbachsengrößen enthalten.

Auf jeden Fall sind wir optimistisch, denn es ist bekannt, dass die elliptischen Funktionen doppelt periodische Funktionen sind, so dass die Möglichkeit, noch weitere Quantenzahlen außer der schon eingeführten Hauptquantenzahl zu „entdecken”, durchaus nicht aussichtslos erscheint - nein im Gegenteil sogar erwartet werden muss. Ja, aus der doppelten Periodizität der elliptischen Funktionen folgt sogar zwangsläufig, dass es keine zwei - voneinander unabhängige neue Nebenquantenzahlen zu entdecken gibt, sondern dass nur noch eine unabhängige Nebenquantenzahl gefunden werden kann; die andere muss dann zwangsläufig einer einfachen Relation von Haupt- und unabhängiger Nebenquantenzahl genügen. Wir werten diesen „seltsamen Zufall” natürlich als Indiz im Sinne unserer Hypothese. Doch schon nach dem Versuch des Aufschreibens der hier zu lösenden Bestimmungsgleichung für die Halbachsenverhältnisse wird der oben geäußerte Optimismus gewaltig gedämpft.

Das hieße nämlich eine Gleichung als Bestimmungsgleichung für die Halbachsen auflösen; die schon beim Aufschreiben völlig unübersichtlich wird. Selbst die Angabe dar Funktionen in einer solchen Gleichung ist schon derart verworren und führt auf elliptische Integrale mit unerhört komplizierten Integranden, so dass an eine elementare Lösung nicht mehr zu denken ist, besonders, wenn man bedenkt, welche Hilfsmittel hierzu benötigt werden (auf die der Verfasser selbstverständlich nicht zurückgreifen kann). Diesen Beweis bleiben wir also schuldig und hoffen, dass er später nachgeholt werden kenn (Wir werden in den Schlussbemerkungen dazu noch einmal Stellung nehmen).

Im Folgenden wenden wir uns nun dem Aufbauprinzip des Atoms zu und fragen, ob unser Modell auch hier anschauliche, mit der Natur übereinstimmende Resultate liefert. Wir stellen uns nun also - entsprechend dem bereits bekannten Verfahren - einen nackten Kern vor, der nacheinander Elektronen einfängt. Beim Wasserstoff und beim Helium brauchen wir nicht mehr zu diskutieren, denn diese beiden Fälle haben wir bereits - mit Hilfe unserer Erklärung des Pauli-Prinzips als übereinstimmend mit den tatsächlichen Verhältnissen gefunden, wesentlich interessanter wird die Fragestellung beim Lithium.

Zunächst stellen wir fest, dass die beiden auf der 1s-Bahn umlaufenden Elektronen das außen umlaufende 2s-Valenzelektron nicht bemerken, denn sie befinden sich in jedem Falle innerhalb der durch die 2s-Bahn erzeugten Kugelschale und damit in Bereich der „magnetischen Windstille”. Jetzt fragen wir: „Bemerkt” nicht aber das 2s-Elektron die beiden 1s-Elektronen? Hierbei können zwei Möglichkeiten eintreten: Wir diskutieren zuerst die Möglichkeit, dass das 2s-Elektron in Richtung e - f mit der Spinrosette in Wechselwirkung treten kann.



Diese Möglichkeit der Wechselwirkung ist aber ausgeschlossen, weil beide 1s-Elektronen gleichzeitig einen Umlauf beenden und dadurch ihre magnetischen Felder sich gerade aufheben. Die zweite Möglichkeit wäre die, dass das 2s-Elektron die eigene Wechselwirkung eines 1s-Elektrons z.B. in Richtung 1 „bemerkt” und mit seiner eigenen Wechselwirkung irgendwie "koppelt". Das wäre der Fall, wenn die Umlaufszeiten des 1s- und des 2s-Elektrons gleich wären wegen des Magnetfeldsatzes. Da das aber nicht der Fa11 ist, treten auch hier keine „Störungen” auf. Doch wir bleiben zunächst bei dem Gedanken, dass eigene Wechselwirkung eines Elektrons eventuell mit der eigenen Wechselwirkung eines anderen Elektrons „gekoppelt” sein könnte. Das wäre nämlich dann der Fall, wenn die beiden Elektronen nicht zum gleichen Kern gehören würden. Da wir fordern müssen, dass beide die gleichen Umlaufszeiten haben müssen, also beide Elektronen in ihren Haupt- (und sicher auch Neben-) quantenzahlen übereinstimmen müssen, wäre hier vielleicht die Erklärung für eine reine homöopolare Bindung gegeben, z.B. für die H₂-Molekel? Wir wissen aber nach den Aussagen der Quantentheorie, dass dabei eine antiparallele Spin-Einstellung Voraussetzung ist. Nun, auch damit müssen wir rechnen, denn bei antiparalleler Stellung von zwei Spin-Rosetten hat das H₂-Molokül seinen Anteil der fremden Wechselwirkung verkleinert, ist also edelgasähnlicher als das einzelne Atom. Wir stellen also fest, dass das Elektron die „ungestörte” eigene Wechselwirkung oder „schwach gestörte” oder gekoppelte eigene Wechselwirkung der fremden Wechselwirkung „vorzieht”. Wie sieht nun eine solche „Kopplung” aus, wenn die Spinrosetten antiparallel stehen? Es tritt das Gleiche ein, was wir schon bei der Supraleitung diskutierten: Beide Elektronen laufen im gleichen Umlaufssinn um Richtung 1! Wir erhalten also bei gekoppelter eigener Wechselwirkung ein Resultat, das genau entgegengesetzt zur Lenz´schen Induktionsregel steht: Gekoppelte eigene Wechselwirkung erzeugt nur dann Anziehung, wenn der Umlaufssinn und die Umlaufszeit um die Raumrichtung, in der Kopplung vorliegt, für beide Partner der gleiche ist. Dieses Resultat müssten wir erwarten, denn sonst könnte sie (die eigene Wechselwirkung) nicht unter diesen Bedingungen existieren. Und genau das Resultat liefert ja auch die Quantentheorie: Bei paralleler Spinstellung der Partner entsteht Abstoßung. Demnach schreiben wir nun folgenden Satz:



Nun können wir mit den gleichen Argumenten die Ionenbindung erläutern: Ein Platzwechsel wird zugunsten der „schwach gestörten” eigenen Wechselwirkung vorgenommen. Doch wir sind etwas vom Thema abgekommen und kehren zum Lithium zurück. Wir können nun weitere Elektronen hinzufügen und wissen, dass jede Kugel und jeder Ellipsoid erst mit zwei Elektronen besetzt sein soll, bis der nächste aufgebaut wird. Allerdings kann nun der Fall eintreten, dass stark exzentrische Bahnen auch einmal aus diesem Gebiet der magnetischen Windstille ausbrechen und nun das - gegen fremde Wechselwirkung ungeschützte äußere S-Elektron „bemerken” (Abb. 24). Also müssen wir fordern, dass diese Bahnen nicht besetzt werden dürfen, sondern dass zuerst die Bahn vom s-Typ (Kugeltyp) voll besetzt werden muss, damit sie gegen fremde Wechselwirkung geschützt ist.

Diese „Faustregel” versagt zuerst beim Chrom, dann beim Kupfer und wird schließlich vom Niob an immer häufiger verletzt. Das liegt daran, weil wir hier das Vielteilchenproblem sicher nicht mehr mit einer solch einfachen Regel erklären können - ja es gar nicht mehr übersehen. Wir können also zusammenfassend feststellen, dass unsere Deutung des Aufbauprinzips ebenfalls als Indiz für die Richtigkeit des bisher dargelegten Weges gelten darf. An dieser Stelle sei dem Verfasser gestattet, einige Bemerkungen einzuflechten: Durch die große Zahl der Gänsefüßchen wird dem Leser sicher nicht entgangen sein, dass dem Elektron, das sich im Zustand der eigenen Wechselwirkung befindet, eine gewisse Individualität zugesprochen wird. Man möge diese Art der Beschreibung nur so verstehen: Wir suchen zielstrebig nach einem universellen Extremalprinzip, das beide Wechselwirkungsmechanismen (eigene und fremde) enthält und das uns gestattet, alle Naturvorgänge soweit wie möglich einheitlich zu beschreiben. Für diese Aufgabe sammeln wir Material und wählen deshalb diese Art der Beschreibung, Damit wir nämlich ein solches Prinzip angeben können, ist es notwendig, dass wir folgende Frage beantworten: Durch welchen Anlass oder durch welche Ursache wird eindeutig entschieden, für welche Art von Wechselwirkung sich das Elektron „entscheidet”? Nur aus diesem Grunde sind wir zur Zeit noch nicht in der Lage, dynamische Vorgänge im Atom zu erläutern (- zum Beispiel ein anschauliches und kausales Modell des Abstrahlungsmodus eines Lichtquants zu geben). Wir fahren also zunächst mit dem Sammeln von Indizien fort.

Wir nehmen nun zu einer weiteren Frage Stellung: Wenn die Berechnung des Planck'schen Wirkungsquantums richtig ist, dann ist der auf heuristischem Wege gefundene Ansatz:

   Eigenwechselwirkungsenergie
   eines Teilchens     = E_w = m_oc²



ebenfalls von ungeheurer Tragweite, denn nun erscheint die Ruhemasse eines geladenen Teilchens (wenn wir konsequent sind und E_w als Ergebnis einer Bahnvorschrift betrachten) als variable Größe, denn erstens ist dies sicher nicht die einzige Bahnvorschrift, die existiert und zweitens wollen wir die Lichtgeschwindigkeit als universelle Naturkonstante nicht anzweifeln. Und in der Tat, es existiert - ähnlich der Sommerfeld-schen Feinstrukturkonstante (die unsere Zweifel an der Universalität von h bestärkte) - eine Beziehung, die diesen Gedanken nicht absurd erscheinen lässt; Das konstante Verhältnis der Ruhemassen von Elektron und Proton. Sollte etwa dieses Verhältnis das Ergebnis zweier Bahnvorschriften ein und desselben Teilchens - nur mit unterschiedlichem Ladungsvorzeichen - sein? Nun, wir schrecken. nicht vor einem solchen Gedanken zurück, denn wir müssen auf alle Fälle erwarten, dass unsere kausale Betrachtungsweise - wenn sie von sich behauptet, mehr zu leisten als die Quantentheorie, auch in der Lage ist, den Kern zu erklären. Noch ein zweiter Gedankengang führt ebenfalls zur vollen Berechtigung dieser Fragestellung:
Wir haben bisher die eigene Wechselwirkung für ein Elektron studiert, das - durch die Coulomb-Anziehung des Kernes - gezwungen war, auf einer vorgegebenen Kugelschale oder auf der Oberfläche eines Ellipsoides zu verbleiben. Diese eigene Wechselwirkung ist also „unfrei”. Wir fragen deshalb mit vollem Recht: Was geschieht, wenn wir das Elektron von dieser Fessel befreien und es - vollkommen frei - mit sich selbst in Wechselwirkung treten lassen? Es müsste also solch ein Mechanismus auffindbar sein, wenn wir konsequent den nun einmal beschrittenen Weg weiterverfolgen. Wir können noch aus einer dritten, äußerst interessanten Sicht den erratenen Ansatz E_w = m_oc² beleuchten:
Es ist bereits schon allgemein angewandte Praxis in der Kernphysik, dass Massen in Energien umgewandelt werden und umgekehrt. Damit hat die Ruhemasse eines Teilchens (in der alten klassischen Vorstellung als „Klumpen Materie”) schon längst ihre Vorstellungsbasis verloren und erscheint als komprimierte Energie. Das ist ganz und gar nicht verwunderlich, denn es gibt schon längst genügend Anhaltspunkte dafür, dass auch der Atomkern (ähnlich der Hülle) leer ist. So können ja z.B. die „kernfremden” Teilchen viele Kerne ohne Wechselwirkung durchqueren. Aus dieser Sicht ist der Ansatz

E_w = m_oc²

sogar der Schlüssel zum physikalischen Verständnis der Einsteinschen Masse-Energie-Beziehung und wir formulieren:

Die ungeheuren Energien, die die Kernenergien darstellen, sind also eigene Wechselwirkungsenergien? Doch wir wollen zu unserer Aufgabe zurückkehren: Wir stellen uns also die Aufgabe, einen oder mehrere freie eigene Wechselwirkungsvorgänge zu entdecken. Wir erwarten, dass das Ergebnis dieser Untersuchung ein oder mehrere Elementarteilchen sind. Dazu tragen wir noch einmal das Material zusammen, das wir bisher (völlig unbewusst) gesammelt haben. Wir rufen uns also einen Satz ins Gedächtnis, den wir ganz zu Anfang unserer Ausführungen machten. Wir stellten fest, dass die Taumelbahn, die das Elektron auf der Kugelschale abläuft, stückweise eben ist. Das ist auch bei der Taumelbahn auf dem Ellipsoid der Fall, wenn wir von der geringfügigen relativistischen Periheldrehung (die die Quantentheorie berechnet) absehen. Wir versuchen uns also mit einem Bahnmodell, das ebenfalls stückweise eben sein soll. Natürlich muss solch eine Bahnkurve stetig und geschlossen sein. Ebenso fordern wir, dass diese Bahn überall knickfrei ist. Weiterhin sollen - in Analogie zum bisherigen Modell-Raumrichtungen existieren, die von stetigen - und in der räumlichen Ableitung stetigen Bahnkurventeilen umschlossen werden, wobei wenigstens Teile der Bahnkurve in dieser Raumrichtung parallel zu vorher abgelaufenen Bahnkurventeilen erscheinen. Wir müssen sogar fordern, dass die gesamte, zu suchende Raumkurve sich lückenlos aus solchen Teilen der eigenen Wechselwirkung zusammensetzt, sonst muss ja unser „Teilchen” sofort „zerplatzen”. Zum Dritten soll in einer Raumrichtung, die keine Richtung der eigenen Wechselwirkung sein darf, unter Umständen auch eine Spinrosette zu erkennen sein, die dem gyromagnetischen Verhältnis des Spin entspricht, also in Analogie zu unserem Modell einen „Vorwärtsdrall mit Rückwärtsgang” darstellt, denn einige Elementarteilchen haben einen Spin. Aber es kommen noch mehr Erwartungen die wir an ein solches Modell stellen, hinzu: Wir erwarten nämlich, wie schon bemerkt, dass nicht nur ein solches Modell existiert, dazu sind unsere Bedingungen viel zu allgemein, Weiterhin hoffen wir, dass sich unsere Modellraumkurven aus Teilen von Kreisen zusammensetzen, denn wir nehmen an, dass sich die Natur bei der Konstruktion ihrer Elementarbausteine rational - bzw. optimal verhalten hat. (Natürlich steht dahinter auch die schwache Hoffnung des Verfassers, nicht wieder auf unlösbare elliptische Integrale zu stoßen). Aber wir hegen noch weitere Hoffnungen: Wir erwarten, dass die freie eigene Wechselwirkung nur auf solchen Raumkurven zustande kommen kann, die auf Kugeloberflächen (oder notfalls Ellipsoidenflächen) liegen, denn wir wollen die Konstanz des Absolutwertes des Drehimpulses (wie wir sie bei der Berechnung von h bestätigt fanden) auch im Bereich der freien eigenen Wechselwirkung gelten lassen. Wir haben nämlich noch keinerlei Anlass zu einer gegenteiligen Annahme.



Nun stellen wir das Spektrum unserer wichtigsten Hoffnungen noch einmal übersichtlich zusammen:

1. Die Bahnkurven. sollen auf Kugeloberflächen (einfachster Fall) Platz finden.


2. Die Bahnkurven sollen aus stückweise ebenen Kreisabschnitten mit jeweils gleichem Radius bestehen.


3. Sie sollen stetig, knickfrei und geschlossen sein.


4. Die Raumkurven sollen sich lückenlos aus solchen Teilen zusammensetzen, die in irgendeiner Raumrichtung eigene Wechselwirkung zulassen, also muss in jedem Punkt der Bahn mindestens eine Raumrichtung existieren, in der ein vorher durchlaufener Bahnabschnitt parallel zum betrachteten Bahnabschnitt läuft und außerdem muss dieser parallele Bahnabschnitt in seiner Fortsetzung eine stetig geschlossene Raumkurve (die dem Magnetfeldsatz genügt) in dieser Raumrichtung ergeben.

Diese Forderungen führen zu den fünf regulären Polyedern, die sich bekanntlich Kugeln einbeschreiben, anbeschreiben sowie umbeschreiben lassen. Da bei diesen Polyedern die Flächen und auch die Ecken kongruent sind, kann man sicher sein, dass ebene Kreisbogenstücke, die den Flächen oder Kanten dieser Polyeder an- bzw. umbeschrieben sind, zu geschlossenen, stetigen und knickfreien Raumkurven führen können. Und in der Tat: Unser bisher studiertes Modell ist ja einem Oktaeder umbeschrieben und gleichzeitig einem Tetraeder anbeschrieben, denn man braucht nur die vier Ebenen, in denen die vier Kleinkreisbögen unseres Modells liegen, zu betrachten und muss erkennen, dass diese vier Ebenen einen Tetraeder aufspannen. Demnach müssen wir annehmen, dass unser - bereits beschriebenes Modell vom Typ: Tetraeder/Oktaeder unter den Elementarteilchen wieder zu finden ist.

Bevor wir aber mit der Konstruktion der Modelle von Elementarteilchen beginnen, wollen wir noch eine fünfte Forderung aufschreiben:

5. Die in irgendeiner Raumrichtung parallel abgelaufenen Bahnstücke der eigenen Wechselwirkung sollen in jedem Falle auch im gleichen Umlaufsinn von geladenen Teilchen durchlaufen werden, denn sonst wäre bei umgekehrtem Umlaufsinn eigene Wechselwirkung nicht vorstellbar.





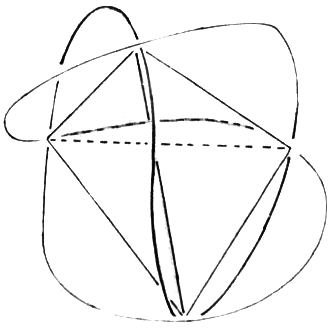
Nun kommen wir zur bereits angekündigten Konstruktion von verschiedenen Elementarteilchen. Zunächst begnügen wir uns mit der Konstruktion der einfach geladenen Elementarteilchen, indem wir eine Ladung auf den nun folgenden, vorgeschlagenen erratenen Bahnkurven laufen lassen.

Wir beginnen mit dem umbeschriebenen Tetraeder. Abb. 25 zeigt die gefundene Lösung, die überhaupt die einzig mögliche - bei Einhaltung unserer Bedingungen - für einen umbeschriebenen Tetraeder darstellt. Wir nennen dieses Teilchen zunächst Tu. Jedes der vier Kleinkreisstücke ist parallel zu einer Polyederkante (1,2), wobei vier der Tetraederkanten „ausgelassen” werden und nur zwei gegenüberliegende Kanten für diese Parallelität je zweimal beansprucht werden. Dadurch ist die Raumrichtung, die senkrecht auf diesen bevorzugten Kanten steht, gegenüber anderen Richtungen ausgezeichnet und wir zeigen den Blick in dieser Richtung sogleich in Abb. 26. Wir müssen feststellen, dass diese vier, hier stetig ineinander übergehenden Ellipsen eine neue Art von „Spinrosette” darstellen, denn nun berühren sich diese Ellipsen nicht mehr in der Mitte, sondern überlappen sich, so dass unser „Vorwärtsdrall mit Rückwärtsgang” verloren gegangen ist. Mehr wollen wir an dieser Stelle nicht feststellen, denn wir sind im gegenwärtigen Stadium der Untersuchung unserer Modelle noch gar nicht in der Lage, den „Spin” etwa ähnlich unserem bisher angewandten Verfahren auszurechnen. Die Ursache dafür liegt in der Tatsche begründet, dass wir bei der Angabe des mittleren Drehimpulses um solch eine Achse ja gezwungen sind, Massen anzugeben. Nun haben wir aber gerade erst festgestellt, dass Ruhemasse und eigene Wechselwirkungsenergie direkt voreinander abhängen, so dass wir erst dann zu einer genauen Angabe des Spin gelangen können, wenn wir mehr über die Ruhemassen unserer Teilchen wissen. Wir werden also (als Ersatz für den „Spin”) den Begriff des „Vorwärtsdralles mit Rückwärtsgang” benutzen, um später leichter unsere Teilchen identifizieren zu können und erwarten, dass das Verhalten in dieser ausgezeichneten Richtung als Spinersatz gelten darf. Nun zeigen wir in der nächsten Abbildung 27 eine der vier Richtungen der eigenen Wechselwirkung.





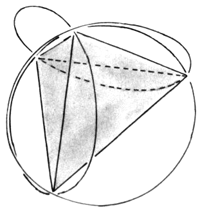
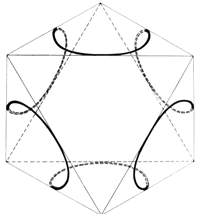
An dieser Stelle brechen wir erst einmal ab und stellen weitere Teilchenmodelle vor. Unser bereits bekanntes Modell des umbeschriebenen Oktaeders bzw. den anbeschriebenen Tetraeders wollen wir unverändert (wie schon angekündigt) mit übernehmen - lediglich lassen wir den Kern natürlich weg und stellen uns unsere Bahn viel kleiner als bisher vor. Dieses Teilchen, das einen „Vorwärtsdrall mit Rückwärtsgang” hat, wollen wir TaOu nennen.

Da wir nun den von Kreisen anbeschriebenen und umbeschriebenen Tetraeder sowie den umbeschriebenen Oktaeder gefunden haben, suchen wir nun nach einem mit Kreisen anbeschriebenen Oktaeder. Dieses Teilchen, das Abb. 28 zeigt, nennen wir Oa. Jeder der sechs Kreisbögen liegt in einer Oktaederfläche, allerdings werden hier zwei der 8 Oktaederflächen ausgelassen. Dadurch entsteht wieder eine bevorzugte Raumrichtung, nämlich die, die auf beiden ausgelassenen Dreiecken senkrecht steht. Blicken wir nun in dieser Richtung durch unser Modell (Abb. 29), erkennen wir deutlich einen „Vorwärtsdrall mit Rückwärtsgang”. Diese Rosette hat sich nun in umgekehrter Richtung entfaltet, als das beim Teilchen Tu der Fall war, sie hat sich gewissermaßen geöffnet, statt geschlossen. In dar nächsten Abbildung (Abb. 30) zeigen wir nun eine der Richtungen der eigenen Wechselwirkung.

Nun kommen wir zum nächsten Polyeder, dem Würfel. Hier finden wir nur eine Lösung, nämlich den anbeschriebenen Hexaeder (Abb. 31), den wir Ha bezeichnen wollen. Abb. 32 zeigt die Spinrosette mit dem „Vorwärtsdrall mit Rückwärtsgang” und Abb. 33 zeigt die Richtung der eigenen Wechselwirkung.



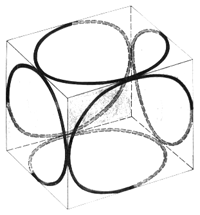
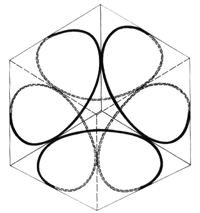
In den folgenden drei Bildern wird nun der anbeschriebene Dodekaeder mit „Spinrosette” und eigener Wechselwirkungsrichtung gezeigt, (Bezeichnung Da), Abb. 34, 35 und 36.

Weiterhin haben wir noch den anbeschriebenen Ikosaeder (la) (Abb. 37 bis Abb. 39) und den umbeschriebenen Ikosaeder (Iu) vorzustellen (Abb. 40 bis Abb. 42). Der anbeschriebene Ikosaeder Ia hat wieder einen „Vorwärtsdrall mit Rückwärtsgang”, während der umbeschriebene Ikosaeder analog unserem Teilchen Tu keinen derartigen Drall in seiner „Spinachse” zeigt. Trotz eifriger Bemühungen gelang es nun nicht, ein Modell für den umbeschriebenen Dodekaeder und (wie schon bemerkt) für den umbeschriebenen Hexaeder zu finden, so dass die Gesamtzahl unserer einfach geladenen Elementarteilchenmodelle 7 beträgt, denn weitere Modelle wurden nicht gefunden. Im Übrigen enthält die von Joos, Lehrbuch der Physik, 10. Auflage angegebene Tabelle der Elementarteilchen sechs einfach geladene Teilchen und ein umgeladenes Teilchen deutlich verschiedener Ruhemasse.

Zum Zwecke einer Identifizierung stellen wir nun erst einmal zwei Tabellen auf, eine Tabelle mit Merkmalen der von der Natur vorgegebenen Elementarteilchen und eine Tabelle mit Merkmalen unserer Modelle. Dabei werden nur die schweren Elementarteilchen erfasst, ebenso geben wir keine Ladungszeichen, keine Ruhemassen und keine Anti-Symbole an, um das, was wir zeigen wollen, übersichtlich darzustellen.








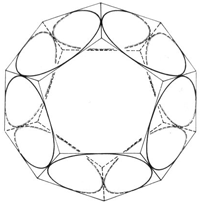
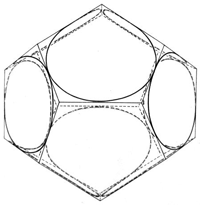
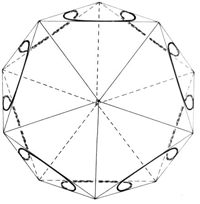
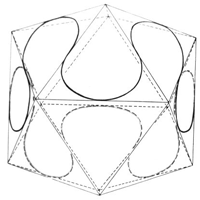
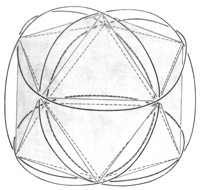
1. Tabelle v. Joos

Elementarteilchen	Spin	besondere Kennzeichen
μ	½	tritt nur in geladenem Zustande auf, „kernfremdes Teilchen”
π	0
K	0
p	½	Lebensdauer unendlich
λ	½	bisher nur ungeladen bekannt
Σ	½
Θ	½

2. Modelltabelle

Teilchenmodell	Vorwärtsdrall mit Rückwärtsgang	besondere Kennzeichen
Tu	nein
TaOu	ja	ist gleichzeitig zwei regulären Polyedern kongruent Bahnrosette berührt als einzige Spinachse
Oa	ja
Ha	ja	Die Bahnkurve lässt keine der Polyederflächen oder Kanten aus
Da	ja
Ia	ja	Die Bahnkurve lässt die meisten Polyederflächen (zehn von zwanzig) aus
Iu	nein



Betrachtet man nun beide Tabellen aufmerksam, so kann man gewisse Verwandtschaften feststellen. Wenn wir die Spalte „Vorwärtsdrall mit Rückwärtsgang” in der zweiten Tabelle mit „Spin” übersetzen, so finden wir - genau wie in der Tabelle 1 - zwei Teilchen, die keinen „Spin” haben. Allerdings müssen wir nun einräumen, dass unser Magnetfeldsatz einer Korrektur bedarf, die wir später nachholen werden. Ebenso enthält die Spalte „besondere Kennzeichen” in beiden Tabellen je drei Teilchen, die durch ihr extremes Verhalten gegenüber allen anderen Teilchen hervorstechen. Diese Teilchen haben in beiden Tabellen den „Spin ½”; es tritt also keine „Überschneidung der Eigenschaften” ein. Offensichtlich sind wir also auf dem richtigen Wege. Durch diese Indizien kühner geworden, beginnen wir nun sogleich unsere Modelle zu identifizieren. Wir ordnen also das Modell TaOu dem μ-Meson zu, weil es wegen seiner kernfremden (hüllenfreundlichen) Eigenschaften genau in unser Konzept passt. Nach unserer bisherigen Auffassung ist es ja nichts weiter als ein verkleinertes Modell aller Elektronenbahnen um den Kern. Ebenso fällt es nicht schwer, das Modell Ha dem Proton zuzuordnen, denn hier ist ein Höchstmaß an Symmetrie und völliger „Auslastung” aller Polyederflächen gegeben. Nun bleibt unter den Teilchen, die besondere Kennzeichen trugen, nur noch das Teilchen λ übrig und wir ordnen ihm das Modell Ia zu.
Nun wissen wir aber, dass π- und μ-Meson recht wenig verschiedene Ruhemassen haben. Gleichzeitig erkennen wir, dass das Modell TaOu und das Modell Tu sehr große Ähnlichkeit miteinander haben - ihre eigenen Wechselwirkungsenergien - und damit ihre Ruhemassen - dürfen sich also nur wenig unterscheiden. Mit dieser Analogiebetrachtung als Hilfe ordnen wir also dem spinlosen Teilchen π das Modell Tu zu.
Damit bleibt nur noch ein spinloses Teilchen, das K-Meson übrig und diesem ordnen wir nun notgedrungen das Modell Iu zu.
Lediglich die Modelle Da und Oa können wir zunächst nicht in unser Schema der Eigenschaften pressen; wir hoffen, dass eine Unterscheidung später gelingen wird, wenn die Ruhemassen dieser Teilchen berechenbar sind.

Wir stellen nach dieser Abhandlung mit Genugtuung fest, dass unsere Analogiebetrachtungen insgesamt dafür sprechen, dass wir uns den Elementarteilchen auf die Spur geheftet haben, denn man hätte ja auch ebenso gut 1000 Modelle finden können. Ebenso stellen unsere „Eigenschaftsbeziehungen” eine Brücke zwischen den Modellen und den Teilchen dar, die zwar noch unsicher und schwankend erscheint, aber immerhin zu recht vernünftigen Vorstellungen führen kann. Selbstverständlich kann jeder Kritiker an dieser Stelle bemängeln, dass unser Vorgehen nicht sauber ist, denn wir haben bis jetzt mit, keinem Wort z.B. zu den ungeladenen Teilchen Stellung genommen. So kann unser Stapeln von Indizien demnach zunächst den äußeren Anschein haben, als wollten wir - nur um den tatsächlichen Verhältnissen angepasste Modelle vorzustellen - mit diesen Indizien alle inneren Widersprüche unserer Auffassung auffangen.



Dieses Argument ist sicher völlig richtig, wenn der Verfasser den Anspruch erheben wollte, eine in jedem Detail hieb- und stichfeste Theorie vorzustellen. Gerade das ist aber nicht Sinn und Zweck dieser Arbeit, denn dann müsste am Anfang aller Betrachtungen z.B. eine Gleichung oder ein universelles Prinzip stehen, aus dem alle anderen Spezialfälle abgeleitet werden können. Diesen Anspruch erheben wir nicht. Erstens ist es im Allgemeinen sehr schwer für den Leser, einer solchen Verfahrensweise zu folgen und zweitens will diese Arbeit in keiner Weise den Anspruch auf Vollständigkeit bzw. Exaktheit in jeder Richtung erheben. Sie soll lediglich Anlass sein, einige wesentliche Punkte der modernen Quantentheorie einmal von einer anderen Seite her zu beleuchten. Außerdem ist das Gebiet der Quantentheorie so ungeheuer angewachsen, dass es gar nicht möglich ist, in solch einem Rahmen alle angerissenen Probleme vollständig zu behandeln. Deshalb erscheint uns dieser Weg der Darstellung als der interessanteste, reizvollste - und im Übrigen auch verständlichste. Übrigens erinnern wir noch einmal daran, dass wir am Anfang unseres kleinen physikalischen Rätselratens eine gewisse Willkürfreiheit beanspruchten. Jedenfalls können wir bis hierher in Anspruch nehmen, dass wir dem Kausalitätsprinzip treu geblieben sind und setzen daher unsere Bemühungen fort:

Es wird nun allerdings Zeit, dass wir zu den ungeladenen Teilchen Stellung nehmen bzw., diese in unser Modellbild aufzunehmen. Für dieses Unternehmen schauen wir noch einmal kurz zurück auf unsere beiden Tabellen der Elementarteilchen. Dort hatten wir das Modell TaOu mit dem μ-Meson auf Grund seiner „Hüllenfreundlichkeit” identifiziert. Andererseits ist ja bekannt, dass das μ-Meson kein ungeladenes Schwesterteilchen kennt.
Nun betrachten wir das λ-Hyperon, das wir mit dem Modell Ia identifizieren. Dieses Teilchen tritt nur in der ungeladenen Form auf.
Wir haben also in beiden Elementarteilchen se etwas wie Extremfälle bezüglich der Bildung von geladenen und ungeladenen Schwesterteilchen vor uns.
Nun betrachten wir die beiden dazugehörigen Teilchenmodelle TaOu und Ia in ihren Spinrichtungen und müssen erkennen, dass auch hier zwei Extremfälle vorliegen. Während beim Modell TaOu alle Bahnkurventeile (lies Kreisbogenstücke) durch die Spinachse gehen (übrigens ist das bei keinem anderen Modell der Fall), entfernen sich diese beim Modell Ia am weitesten von allen Modellen von der Spinachse.
Dienen wichtigen Hinweis werden wir bei der Konstruktion unserer ungeladenen Elementarteilchen verwenden.
Wir stellen nun eine ähnliche Frage, wie wir sie zu Anfang unserer Arbeit bei der Erläuterung des Pauli-Prinzips formulierten: Wieviel Ladungen passen noch auf eine Kugelschale, auf der solch eine Ladung sich schon im Zustand der freien eigenen Wechselwirkung befindet und welchen Vorschriften sind diese Ladungen unterworfen?



Wir begründen zuerst, dass diese Fragestellung richtig ist, dass wir also weitere Ladungen nur auf der Kugelschale selbst zulassen dürfen. Wir wissen, dass nur eine Elementarladungsstärke (mit positivem oder negativem Vorzeichen) in der Natur existiert. Lassen wir nun noch irgendeine zweite Ladung z.B. im Innenraum der vorgegebenen Kugel auf irgendeiner Bahn zu, dann haben wir praktisch den Fall der teilweisen unfreien eigenen Wechselwirkung vorliegen, den wir aber nicht für die Elementarteilchen beanspruchen wollen. Das Gleiche gilt, wenn wir eine zweite Ladung (ebenfalls ist es gleichgültig, welches Vorzeichen diese führt) im Außenraum um die vorgegebene Kugel zulassen, dann tritt wiederum das Gleiche ein. Mit dieser Erklärung haben wir viel mehr dargestellt, als wir erwarteten, denn nun können wir ohne weiteres aufschreiben:

Dieser - probeweise aufgeschriebene Satz - ist eine ganz allgemeine Formulierung des Pauli-Prinzips und gilt gleichermaßen für alle stabilen Zustände in der Hülle sowie für die Elementarteilchen, was wir noch überprüfen werden. Wir vermuten sogar sehr stark, dass dieser Satz einen Teil des universellen Extremalprinzips (was wir suchen!) darstellt und ganz allgemein gültig ist. Wir nennen diesen Satz den Stabilitätssatz.

Doch nun wollen wir die Bedingungen erarbeiten, denen die noch auf der Kugelschale zugelassenen weiteren Ladungen (außer der schon dort befindlichen Ladung) unterworfen werden müssen:

1. Sie müssen sich ebenfalls im Zustande der (angenähert) freien eigenen Wechselwirkung befinden.


2. Die Umlaufszeiten müssen gleich der Umlaufszeit sein, die die schon dort befindliche Ladung hat, denn sonst beginnen diese Ladungen - ganz analog zu unseren Beschreibungen der homöopolagen Bindung - sich irgendwann gegenseitig zu ''bemerken” und das Teilchen zerfällt. Mit diesen zwei Bedingungen und der Forderung nach Aufenthalt auf der gleichen Kugelschale steht fest: Die zusätzlich zum Teilchen noch zugelassenen Ladungen dürfen nur noch auf derselben Bahn umlaufen, die die schon vorhandene Ladung vorgezeichnet hat.



Aber noch mehr ist abzulesen: Dazu setzen wir zwei Ladungen auf zwei beliebige Orte solch einer Bahn, schicken sie auf die Reise und wählen für beide das gleiche Vorzeichen. Wenn wir sie nun im genau entgegen gesetzten Umlaufsinn auf ihren Weg schicken, wäre binnen kurzem ein Zusammenprall oder ein gegenseitiges Durchdringen (denn wir wissen noch zu wenig über die Ladungen an sich) nicht zu vermeiden. Für dieses Gedankenexperiment aber haben wir auf jeden Fall keine Erfüllung der Stabilitätsforderung vor uns und verwerfen demnach diese Lösung als nicht stabil.

Nun schicken wir beide Ladungen zum zweiten Male auf die Reise; wir wählen wieder das gleiche Vorzeichen, diesmal aber den gleichen Umlaufsinn für beide Partner. Nach kurzer Zeit werden sich beide wegen der Coulomb-Kräfte der fremden Wechselwirkung - auf äquivalenten Teilen der Bahn gegenüberstehen und wir hätten nun scheinbar ein Minimum der zeitlichen Änderung der fremden Wechselwirkung. Doch ist dies leider nicht der Fall, denn wir erkennen überhaupt kein Argument, wodurch denn diese zwei Ladungen eigentlich zusammenhalten sollten. Somit ist auch diese Lösung zu verwerfen und wir formulieren (was wir ja schon längst wissen): Es gibt kein Elementarteilchen, das zwei- oder mehrfach geladen ist.
Nun beginnen wir unser Spiel von neuem, diesmal bringen wir zwei Ladungen mit entgegen gesetztem Vorzeichen, aber umgekehrtem Umlaufsinn auf unsere Bahn. Auch diese Lösung erscheint - weil sie nicht den Stabilitätssatz erfüllt, als nicht stabil.
Zuletzt fragen wir nach dem Verhalten von zwei Ladungen mit entgegen gesetztem Vorzeichen, die wir mit dem gleichen Umlaufsinn auf die Reise schicken. Wenn beide Ladungen nun so starten, dass ihre durch beide hindurchgehende Sekante nicht durch den Mittelpunkt der Kugel geht, wenn mit anderen Worten die beiden Ladungen sich nicht in jedem Falle diametral gegenüberstehen, werden sie sich laufend annähern und der Stabilitätssatz wird wiederum nicht erfüllt. Lassen wir nun aber beide Ladungen sich in jedem Punkte der Bahn genau gegenüberstehen, dann beginnen sie sich zu „jagen”, ohne sich erreichen zu können. Man könnte also nun annehmen, dass ein solches Modell, das den Stabilitätssatz erfüllt, ein neutrales Elementarteilchen darstellt (Im Übrigen ähnelt dieses Modell sehr stark unseren in der Hülle vollbesetzten Kugelschalen).
Aber man sieht leicht ein, dass solch ein Modell auf jeden Fall nicht stabil sein kann, weil die beiden Ladungen, sofern die nur gering von der diametralen Konstellation abweichen, sich sogleich einander nähern müssen und dann haben wir den oben beschriebenen Fall.



Wir können also mit Genugtuung feststellen, dass das Stabilitätstheorem auf die Lösung führt, die ja bekannt ist: Es gibt nur labile neutrale Elementarteilchen. Nun werden wir überprüfen, ob unser hier vorgestelltes Modell eines ungeladenen Elementarteilchens auch eine mit der Erfahrung übereinstimmende Aussage bezüglich der anderen Eigenschaften der ungeladenen Teilchen liefert. Das gelingt am besten, wenn wir unsere in der Tabelle 2 angegebenen Modelle einzeln unter Einhaltung der eben erarbeiteten Vorschrift untersuchen. Wir beginnen mit dem μ-Meson (Modell TaOu). Wenn hier zwei Ladungen. mit entgegen gesetztem Vorzeichen diametral und im gleichen Umlaufsinn die vorgeschlagene Modellbahn ablaufen, dann findet ihr gemeinsamer Lauf nach einem vollen Umlauf ein jähes Ende, dann beide vollenden gleichzeitig je eine Spinrosette, die völlig deckungsgleich sind. Die Magnetfelder der fremden Wechselwirkung aber verhindern nun den ungestörten Weiterlauf beider Teilchen. Der Stabilitätssatz ist nicht erfüllt und wir dürfen - in voller Harmonie mit den natürlichen Verhältnissen - sagen, dass es kein ungeladenes μ-Meson geben darf.

Nun wenden wir uns dem π-Meson (Modell Tu) zu. Wir blicken in Richtung der Spinachse und lassen nun beide Ladungen - wie vereinbart - diametral im gleichen Umlaufsinn starten. Aber schon ergeben sich Schwierigkeiten: Durch die Eigenart der hier vorgestellten Bahnvorschrift gibt es nämlich nur zwei Konstellationen der beiden Elektronen, bei denen die Elektronen wirklich diametral stehen. An allen anderen Punkten der Bahn geht die gemeinsame Sekante dicht am Kugelmittelpunkt vorbei! Der Stabilitätssatz ist also in dieser Richtung nicht erfüllt. Allerdings ist aber die Abweichung der Sekante vom Kugelmittelpunkt eine oszillierende und das Teilchen, das zuerst hinter dem Gegenpunkt des anderen hinterherhinkt, eilt beim nächsten halben Umlauf voraus, so dass man von einem (zwar labilen) Minimum der Änderung der elektrostatischen fremden Wechselwirkung reden könnte. Bezüglich der magnetischen fremden Wechselwirkung besteht keinerlei Anlass zu einer solchen „Katastrophe” wie sie beim μ-Meson vorliegt, denn beide Ladungen beenden einen Umlauf an unterschiedlichen Stellen, so dass ein Zusammenwirken der „Spinmagnete” nicht vorstellbar ist (Im übrigen dürfen wir hier von elektrostatischer und magnetischer Wechselwirkung sprechen, denn wir diskutieren fremde Wechselwirkung, bei der reine elektrische und reine magnetische Energie existieren). Nun betrachten wir Abb. 27 und fragen, ob denn die Magnetfelder der eigenen Wechselwirkung sich gegenseitig beeinflussen können. Diese Frage darf verneint werden, denn jedes Teilchen tritt in jedem Punkte der Bahn in einer anderen Raumrichtung als der Partner mit sich selbst in Wechselwirkung.





Wir fassen nun zusammen: Ein ungeladenes π-Meson sollte außerordentlich instabil sein und in der Tat: Das ungeladene π-Meson hat die kürzeste aller Zerfallzeiten von allen instabilen Elementarteilchen.
Irgend etwas Richtiges muss also an dem Stabilitätstheorem sein, denn wir kommen ja, wenn wir es anwenden, zu recht vernünftigen Aussagen.
Nun fragen wir: Können wir auf der Bahn des Modells Tu (π-Meson) etwa noch weitere Ladungen unterbringen? Wir fügen nun zuerst nur eine Ladung zu dem Pärchen hinzu. Dieses Verfahren muss sofort scheitern, denn nun wird das schon recht labile Oszillieren völlig instabil. Vielleicht aber können wir noch ein weiteres „Pärchen” zu unserem schon vorhandenen hinzufügen, denn wir haben vier unterschiedliche Richtungen der eigenen Wechselwirkung, vielleicht ist bei geschickter Anordnung die Möglichkeit gegeben, dass sich die vier Ladungen nicht bei ihrer eigenen Wechselwirkung gegenseitig beeinflussen! Dazu betrachten wir nebenstehende Abb. 43.
Die Konstellation: 1=e⁺, 2=e⁺, 3=e^-, 4=e^- ist nicht diskutabel, denn nun sind die Ladungen so verteilt, dass in überhaupt keinem Falle mehr die Sekante, die zwei unterschiedliche Ladungen verbindet, wenigstens annähernd zeitlich konstant ist. Wir verwerfen diese Lösung also als nicht dem Stabilitätstheorem entsprechend. Aus ähnlichen Gründen müssen wir auch die Lösung
1=e⁺, 2=e^-, 3=e⁺, 4=e^- verwerfen, denn nun stehen auf dicht benachbarten Bahnsegmenten je zwei gleich geladene Elektronen zeitweise dicht nebeneinander und entfernen sich auch wieder. Aus diesen Gründen können wir feststellen, dass es kein ungeladenes π-Meson geben darf, das bei seinem Zerfall letztendlich in vier einfache Ladungen zerfällt, was ja auch durch die Erfahrung bestätigt wird.

Nun kommen wir zum nächsten Modell, dem anbeschriebenen Oktaeder. Auf jeden Fall gibt es hier ebenfalls ein ungeladenes Schwesterteilchen, wenn ein Paar ( e⁺ und e^- ) Ladungen diametral im gleichen Umlaufsinn diese Bahn besetzt hält. Die fremde Wechselwirkung der magnetischen Energie ist - wegen den gleichen Argumenten, die beim Modell Tu diskutiert wurden, Null und ebenso ist der elektrische Teil der fremden Wechselwirkung ein (labiles) Minimum.





Da wir hier nun sogar sechs verschiedene Richtungen der eigenen Wechselwirkung vorliegen haben, prüfen wir jetzt wieder die Möglichkeit eines Gebildes, das vier Ladungen bzw. sechs Ladungen aufnehmen kann. Der Fall, dass vier Ladungen die Bahn besetzt halten, ist nicht stabil, dann hier entstehen wieder die bereits bekannten elektrischen Asymmetrien (Abb. 44). Aber selbst für die sechs Ladungen finden wir keine Anordnung, die der Forderung des Stabilitätssatzes genügt. Die symmetrischste Lösung ist nämlich folgende: 1=e⁺, 2=e^-, 3=e⁺, 4=e^-, 5=e⁺, 6=e^-. Der dargestellten Abbildung ist sofort anzusehen, dass die Längen der Sekanten, die ein beliebiges Elektron mit den entgegengesetzt geladenen Partnern verbinden, während eines Umlaufes stark variierten, so dass auch diese Lösung als instabil verworfen werden darf. Demnach gibt es nur ein neutrales Schwesterteilchen vom Typ Oa.

Jetzt folgen die gleichen Untersuchungen für das Proton (Ha). Wir können sämtliche Bemerkungen, die beim Modell Oa diskutiert wurden, hier wiederholen, denn beide Modelle gehen durch stetige Deformation und Winkeldrehung ineinander über. Es gibt also nur ein ungeladenes Schwesterteilchen des Protons, das zwei entgegen gesetzte geladene Elektronen enthält. Das ist das Neutron. Nun wenden wir unsere Aufmerksamkeit den Modellen Da und Ia zu. Wir behandeln beide gleichzeitig, denn sie sind auf die gleiche Art wie die Modelle Ha und Oa verwandt. Bei beiden Modellen entdecken wir die Möglichkeit, dass ein ungeladenes Schwesterteilchen existiert, das ein Ladungspaar aufnehmen kann. Weitere Besetzungen dieser Bahn erscheinen nach dem Stabilitätssatz als recht unwahrscheinlich, obwohl - wegen der hohen Anzahl der unabhängigen Richtungen der eigenen Wechselwirkung (insgesamt 10) die Möglichkeit darf dafür gegeben ist. Interessant ist lediglich, dass man (bei gutem Willen!) aus der Bahnkurve des Modells Ia ablesen kann, dass hier vorwiegend die ungeladene Besetzung, selten aber das einfach geladene Teilchen vorkommen darf. Dieses Modell zeigt im Unterschied zu allen anderen Elementarteilchen nämlich keine (wenigstens annähernd gleichmäßige) kugelsymmetrische Ladungsverteilung, sondern das Teilchen pendelt innerhalb eines relativ schmalen Bandes um den Kugelmittelpunkt. Betrachten wir nun Abb. 39, so müssen wir feststellen, dass die eigene Wechselwirkung dieses Modells nicht die ganze Bahnkurve stetig mit solchen festen Raumrichtungen bedeckt, wie das zum Beispiel beim Modell Ha der Fall ist. Wir meinen mit anderen Worten: Eine derartig starke und die ganze Bahnkurve sicher abdeckende Parallelität zwischen vorher durchlaufenem und gegebenem Bahnkurventeil existiert nicht. Vielmehr müssen wir bei diesem Modell die ehemals festen Raurichtungen der eigenen Wechselwirkung gewissermaßen stückweise so drehen, dass ein „Abwälzen” der beiden - für die eigene Wechselwirkung notwendigen Bahnkurven eintritt, so dass die Bedingung des lückenlosen Abdeckens der gesamten Bahnkurve hier nur stückweise gegeben ist.



Betrachten wir nun unter diesem Aspekt alle anderen Modelle, so stellen wir fest, dass - außer unserem Protonenmodell - keines der vorgestellten Modelle diese Bedingung vollständig erfüllt, (doch darauf kommen wir anschließend zurück), jedenfalls ist sie beim Modell Ia am stärksten verletzt. Das geladene λ-Hyperon bedarf also gewissermaßen einer „Stütze”, die es in dem Hinzufügen der zweiten Ladung erhält. Diese zweite Ladung „hilft” gewissermaßen den Bereich der fehlenden Eigenwechselwirkung durch die Coulomb-Anziehunskraft zu „überbrücken”.

Damit aber können wir nun zu einer Erweiterung des Stabilitätssatzes greifen:

Jetzt kommen wir zu der schon angekündigten Behauptung, dass keines der vorgestellten Teilchenmodelle (mit Ausnahme des Protons) diesen erweiterten Stabilitätssatz erfüllt. Wir beginnen mit dem Modell TaOu. Hier ist an acht Punkten der Bahn (nämlich an den Punkten, an denen die eigene Wechselwirkungsrichtung unstetig wechselt) die eigene Wechselwirkung kein konstanter Wert, ihre Änderung ist zwar betragsmäßig konstant, aber ihre Richtung wechselt unstetig.

Die Verhältnisse beim Modell Ia haben wir schon diskutiert, hier existiert ein „Mangel” an eigener Wechselwirkung über bestimmte Teile der Bahnkurve. Das Gleiche gilt für das vorgestellte Modell Oa. Bei den Modellen Tu, Da und Iu dagegen existiert ein „Überschuss” an eigener Wechselwirkung über gewisse Teilbereiche der Bahnkurve. Allerdings ist dieser „Überschuss” nicht so gerichtet, dass er die Ladung auf die vorgegebene Bahnkurve bannt, sondern dieser Überschuss wirkt „ablenkend”. Lediglich beim Proton (Ha) wirkt der „Überschuss” der eigenen Wechselwirkung richtungsgleich und „hält” die Ladung auf der vorgegebenen Bahnkurve, wenn die Richtung der eigenen Wechselwirkung wechselt.
(Diese Betrachtungen kann jeder Leser unschwer selbst durchführen, wenn er die angegebenen Modelle mit Hilfe von etwas Draht herstellt, denn es würde hier zu weit führen, sämtliche für diese Darstellung notwendigen Abbildungen zweidimensional aufzuzeichnen).

Kurz und gut, für unsere Indiziensammlung genügt lediglich die Feststellung, dass wir dem Stabilitätssatz entnehmen dürfen:
Es gibt (- mit Ausnahme des Protons -) kein stabiles Elementarteilchen.



Weiterhin überlassen wir es jedem Leser selbst, nachzuweisen, dass mit Hilfe des Stabilitätstheorems gezeigt werden kann, dass zum Beispiel zwei, vier und sogar sechs (1 Paar, 2 Paare, 3 Paare) Ladungen auf der Bahn des Modells Iu (K-Meson) untergebracht werden können - ebenfalls ein Indiz, das in Übereinstimmung mit der von Joos angegebenen Elementarteilchentabelle steht. Das Pauli-Prinzip der freien eigenen Wechselwirkung lässt also nicht nur zwei Ladungen auf jeder „Schale” zu.

Der Stabilitätssatz aber ist eine wahre Fundgrube; er enthält eigentlich noch wesentlich mehr, denn man kann - wenn man ihn als universell gültig voraussetzt - ohne Schwierigkeiten die Richtungsquantelung beim Stern-Gerlach-Experiment verstehen. Ebenso werden wir ihn nun benutzen, um zu zeigen, dass bei Vorliegen eines fremden Feldes unsere zwei Teilchen ohne „Vorwärtsdrall mit Rückwärtsgang” (π-Meson und K-Meson) ein grundsätzlich verschiedenes Verhalten gegenüber allen anderen Modellteilchen zeigen. Man kann diesen Modellen sofort ansehen, dass alle Richtungen der eigenen Wechselwirkung nämlich als Büschel nahe um die in Abb. 26 und Abb. 41 senkrecht auf der Zeichenebene stehende „Spinachse” gruppiert sind. Unsere beiden Teilchen würden also, wenn sie fremden Feldern begegnen, schlecht beraten sein, gerade diese Achse in Richtung des Fremdfeldes zu drehen, denn jede andere Raumrichtung, die senkrecht auf dieser Achse steht, entfernt die Richtungen dar eigenen Wechselwirkung wesentlich stärker aus der Richtung des Fremdfeldes. Für alle diese Richtungen ist nämlich das Magnetfeld Null, das das Teilchen nach dem Magnetfeldsatz erzeugen darf. Demnach dürfte der Fall, dass die „Spinachse” in Richtung des Fremdfeldes steht, als labiler Zustand praktisch nicht vorkommen. Beide Teilchen also zeigen keinen Stern-Gerlach-Effekt und müssen demnach den Spin Null haben. Dagegen ist für alle anderen Teilchen eine Einstellung der Spinachse in Richtung des Fremdfeldes die stabilste.

Jetzt wenden wir uns den Ruhemassen unserer Teilchenmodelle zu. Selbstverständlich beschränken wir uns zunächst auf die einfach geladenen Teilchen. Mehrere Hinweise kann man bei gründlichem Studium erhalten, wenn man die Frage stellt: Was ist denn nun eigentlich die Ruhemasse eines Teilchens?



Da ist zunächst unsere Bemerkung zu registrieren, dass die Ruhemasse die eigene Wechselwirkungsenergie, geteilt durch das Quadrat der Lichtgeschwindigkeit sein soll. Weiterhin erhält man einen Hinweis, wenn man die Gleichungen betrachtet, die die Paarerzeugung von z.B. Elektron und Positron regieren:

E = m0c²	Ruheenergie einer Ladung
E = h ⋅ ν	Mindestenergie eines (für die Paarerzeugung notwendigen) ∂-Quants

Daraus folgt durch Gleichsetzen:

m0c² = h ⋅ ν = h *	c
	λ

Benutzen wir nun die Gleichung: h = e₀²c ⋅ const, so gilt:

  LI  

m0 = const ⋅	e0²
	λ

Damit erhalten wir den sehr wichtigen Hinweis, dass die Ruhemasse nur von einer einzigen Variablen, die die Dimension einer Länge hat, abhängen muss. Dies ist ein Resultat, das natürlich jeden aufmerksamen Betrachter an die von Heisenberg eingeführte kleinste Länge denken läßt und wir werden sogleich eine anschauliche Begründung für deren Existens versuchen. Für diesen Zweck untersuchen wir eine Ladung. Sie hat die Eigenschaft, Quelle (oder Senke) des Raumes zu sein. Da sie also offensichtlich ein reales, existierendes Objekt ist, das irgendwelche Wirkungen auf sich selbst oder auf andere Ladungen ausüben kann, darf ihre Ausdehnung nicht Null (also gleich dem mathematischen Punkt) sein, sonst wäre sie nicht da. Wenn sie aber endliche Abmessungen besitzt, dann muss es einen kleinsten Krümmungsradius geben, auf dessen Kreisumfang diese Ladung gerade noch in der Lage ist, mit sich selbst in Wechselwirkung zu treten. Dieser kleinste Krümmungsradius könnte die kleinste Länge sein. Da aber die freie eigene Wechselwirkung sicher irgendwelchen Gesetzen folgen muss, gibt es natürlich zu einem solchen kleinsten Krümmungsradius sicher auch eine Umlaufzeit. Diese Umlaufzeit soll die von Heisenberg eingeführte kleinste Zeit sein.



Einen weiteren Hinweis erhalten wir, wenn wir nun zur Kenntnis nehmen, dass ein regulärer Polyeder vollständig bestimmt ist, wenn eine einzige Kantenlänge vorgegeben wird. Nun wissen wir bereits, dass eine Ladung durch eigene Magnetfelder auf den Bahnen der eigenen Wechselwirkung festgehalten wird, deshalb dürfen wir jetzt aufschreiben:

Daraus folgt:

Und in der Tat: Selbst an dieser Stelle verlässt uns nicht die Anschaulichkeit, denn es wäre doch sehr schön anschaulich, wenn man den Ruhemassen (dem Sitz der trägen Massen) Selbstinduktionskoeffizienten zuordnen könnte, die ja geradezu Sinnbild der Trägheit eines Stromverlaufes sind.



Sollte etwa die Analogie zwischen träger Masse einerseits und Selbstinduktion eines Stromkreises andererseits, die in jedem Physiklehrbuch zum besseren Verständnis der Selbstinduktion gegeben wird, gar keine Analogie, sondern tatsächliche Wirklichkeit sein? Eine solche Auslegung ist derart bestechend und harmonisch, dass man gewillt ist, noch mehr Argumente dafür zu sammeln und man muss sich fast davor hüten, damit die Begeisterung für ein solches Vorhaben den klaren Blick nicht trübt. Auf jeden Fall aber könnte eine derartige Auffassung nun tatsächlich der Schlüssel zum Verständnis der Einstein'schen Masse-Energiebeziehung E = m₀c² sein. Damit wir dies zeigen können, schreiben wir drei Gleichungen nebeneinander und diskutieren deren Verwandtschaften:

E = m0c²	Einstein'sche Masse-Energiebeziehung
E =   1   L11 i²  2	Potentielle Energie eines stromdurchflossenen linearen Leiters (Energie der Selbstinduktion)
E = const  e0²  c² λ	Gleichung LI (umgewandelt)

Nun formen wir die zweite Gleichung in üblicher Weise für ein Elektron um:

i =   dq   =   e0 * ds   =   e0   * V  dt s * dt s

s = Gesamtumlaufweg eines Elektrons auf seiner Bahn, die dem Magnetfeldsatz genügt.      V = Geschwindigkeit des Elektrons.

Nunmehr können wir für die zweite Gleichung schreiben:

  LII  

E =   1   L11   e0² * V²  2 s²

dazu schreiben wir:      E = const *   e0²   c²  λ



Betrachten wir nun diese Gleichung und die nochmals aufgeschriebene nebenstehende Gleichung, so stellen wir eine außerordentlich große Verwandtschaft fest. In beiden Gleichungen steht nämlich auf der rechten Seite das Quadrat der Elementarladung, multipliziert mit einer Größe der Dimension cm^-l und dem Quadrat einer Geschwindigkeit. Anscheinend befinden wir uns auf einem Wege, der durchaus die beiden oben aufgestellten Sätze vernünftig erscheinen lässt.
Ja, es folgt aus der Forderung, dass Ruhemasse und Selbstinduktionskoeffizient direkt proportional sein sollen, ein äußerst interessantes Ergebnis :
Es ist ja bekannt, dass der Selbstinduktionskoeffizient völlig unabhängig von der Stromstärke ist und nur von der Geometrie eines Stromverlaufs abhängt. Demnach müssen die Ruhemassen von z.B. Proton und Neutron ziemlich genau gleich groß sein (wenn wir von der geringfügigen Bahndeformation durch Coulomb-Kräfte absehen)!

Mehr aber ist an dieser Stelle noch nicht gestattet, obwohl z.B. ein Gleichsetzen der beiden Gleichungen und damit weiteres Rätseln verlockend erscheint. Das ist deshalb verboten, weil die linke „klassische Gleichung” die Größe L11 enthält, über die wir bisher noch gar nichts ausgesagt haben. Verwendet man nämlich die übliche Formel zur Berechnung der Selbstinduktion einer Ladung, die irgendeine Raumkurve abläuft, dann erleidet man nämlich - genau wie wir bei der Anwendung des Biot-Savart-schen Gesetzes - Schiffbruch, weil diese Formel aus der Betrachtungsweise der fremden Wechselwirkung hergeleitet ist. Wir müssten uns also bemühen, zunächst diese Formel wieder für eine Ladung umzuschreiben - selbstverständlich unter Berücksichtigung unserer bereits gewonnenen Erkenntnisse, speziell des Magnetfeldsatzes.

Wir schreiben aber erst einmal eine solche Formel zur Berechnung eines Induktionskoeffizienten der fremden Wechselwirkung zwischen zwei Leiterschleifen auf:

Und schon entdecken wir ein äußerst wertvolles Indiz: Es ist nämlich „üblich”, dass man die Integrationsrichtungen beider Integrale so wählt, dass L12 positiv wird. Nun werden wir erwarten, dass die Formel des Selbstinduktionskoeffizienten einer einzelnen Ladung auf einer Bahn der eigenen Wechselwirkung ein ähnliches Doppelintegral sein wird. Allerdings sehen wir von unserer Betrachtung her noch kein Argument, warum wir denn in jedem Falle unbedingt so integrieren müssen, dass L11 positiv wird! Da, wir aber schon von fern den Selbstinduktionskoeffizienten mit einer Masse verknüpft sehen, erkennen wir an dieser Stelle die Möglichkeit der Einführung von negativer Masse, also Antimaterie!



Spätestens an dieser Stelle nun erkennt jeder Leser, dass unser Weg sich mehr und mehr verzweigt. Noch haben wir nicht einmal den Versuch der. Ruhemassenberechnung richtig begonnen, und schon fangen wir an, von Antimaterie zu sprechen. Ja, die Flut der nun folgenden Verzweigungen ist derart mannigfaltig, dass uns nun der rote Faden fast unbemerkt entgleitet. Außerdem wachsen die nun zu erstellenden Rechnungen für einen Einzelnen sehr schnell über das noch erträgliche Maß hinaus, besonders dann, wenn man bedenkt, von welcher Warte her diese Betrachtungen entstanden sind. Die letzte Bemerkung versteht der Leser sofort, wenn er die angeführten Literaturen am Ende dieser Arbeit zur Kenntnis nimmt.

Kurz und gut, es wäre an der Zeit, die Feder aus der Hand zu legen, wenn an Hand zahlreicher Verzweigungen gezeigt werden kann, dass der beschrittene Weg in eine fruchtbare Gegend führt, denn dann ist das Ziel dieser Arbeit erreicht. Wir ersparen uns also eine Vielzahl von Beweisen und überlassen diese einem berufenerem Gremium - schon allein deshalb, weil wir zu den aus reiner Unkenntnis (sicherlich schon zahlreich) begangenen Fehltritten nicht noch weitere hinzufügen wollen. Ein solcher Rückzug ist dem professionellen Theoretiker versperrt, für den dilettantischen Amateur dagegen ist er an geeigneter Stelle geboten!

Phantastischer Ausblick

In der vorliegenden Arbeit wird versucht, mit Hilfe des Kausalitätsprinzips in die Welt der Quantentheorie einzudringen und einen Weg vorzuzeichnen, der es gestattet, einige wesentliche Schwierigkeiten der Quantentheorie zu beseitigen, wenn man den bisherigen Standpunkt revidiert. Die Zahl der Beweise für diesen neuen Standpunkt ist gering, dagegen ist Anzahl der Indizien derart erdrückend, dass mit Recht. aufgeschrieben werden darf: Es ist durchaus reizvoll, auch einmal solch einen Standpunkt zu beziehen. So lässt sich zum Beispiel ohne Mühe zeigen, dass der neue Standpunkt durchaus den Postulaten der speziellen Relativitätstheorie entspricht, ja er führt sogar zu einem tieferen Verständnis der allgemeinen Relativitätstheorie, die von der Äquivalenz von träger und schwerer Masse ausgeht. Die in dieser Arbeit angedeutete Massendefinition führt nämlich direkt zu der von Einstein noch als Postulat benutzten o.a. Äquivalenz, wenn man die schwere Masse eines Körpers als ein diffuses „Magnetfeld” auffasst, das von vielen Eigenwechselwirkungen erzeugt wird. Weiterhin existieren nach den Auffassungen des Verfassers nur folgende, physikalisch interessierende Gebilde: Quellen und Senken des Raumes sowie die dazu gehörenden Felder. Diese verhalten sich vermutlich etwa so: Alle dynamischen (zeitlich veränderlichen) Vorgänge entsprechen einem Maximum der zeitlichen Änderung von eigener und fremder Wechselwirkung dagegen entsprechen alle stabilen (zeitlich konstanten) Vorgänge einem Minimum der zeitlichen Änderung von eigener und fremder Wechselwirkung. Dabei müssten alle Vorgänge in einem Maßsystem beschreibbar sein, das mit drei universellen Naturkonstanten auskommt:

1. Lichtgeschwindigkeit
2. Elementarladung
3. Kleinste Länge (oder kleinste Zeit)

Vermutlich wird es also eines Tages gelingen, aus der dritten Naturkonstante die Gravitationskonstante herzuleiten, wie sich auch im Rahmen einer solchen Theorie die Existenz von Gravitationswellen verbietet. Außerdem ist das Unterfangen, die Metrik des Raumes nach den Massenverteilungen zu berechnen, durchaus nicht aussichtslos.



Ebenso darf erwartet werden, dass dann auch einmal Ordnung in die Tabelle der Elementarteilchen gebracht werden kann. Sollte einmal eine solche Theorie geschaffen sein, dann ist auch zu erwarten, dass diese Theorie sicherlich ein vollständiges Bild der Atomkerne liefern kann, denn es wird dann leicht, aus umlaufenen Hexaedern die Kerne zusammenzusetzen, deren „Austauschkräfte” als gekoppelte freie eigene Wechselwirkungen zu erkennen und zu berechnen. Ebenso sind in solch einer Theorie die Massendefekte als Veränderungen von eigenen Wechselwirkungsenergien durch Kopplung sicherlich enthalten und damit ist zu erkennen, dass das große Rätsel der „Kernkräfte” in absehbarer Zeit vielleicht endgültig gelöst werden kann. Ebenso wird diese Theorie die sehr kurze Reichweite der Kernkräfte erklären können. Dass eine solche Theorie auch sicherlich einiges Licht auf die Diskussion „Schalen- oder Tröpfchenmodell” werfen kann, darf nach alledem erwartet werden.

Ebenso darf damit gerechnet werden, dass die Radioaktivität vielleicht in den Bereich der Berechenbarkeit rückt, wenn man annimmt, dass die zum Kern zusammengetretenen Protonen und Neutronen nicht in jedem Falle dem Stabilitätssatz entsprechende Konfigurationen ergeben können.

Weiterhin wird wahrscheinlich eines Tages gezeigt werden können, dass die in der Quantentheorie benutzte Zustandsfunktion Ψ aus der Theorie der elliptischen Funktionen hergeleitet werden kann, denn der Weg des direkten Ausintegrierens der elliptischen Integrale ist im allgemeinen derart mühsam, dass wohl weiterhin die bisher so ergiebige Mathematik bestehen bleiben wird - allerdings nun nicht mehr als beherrschendes Element, sondern als Hilfsmittel zur Erkennung der Natur.

Außerdem wird eine solche Theorie vielleicht auch einige neue Ausblicke auf solch „rätselhafte” Naturerscheinungen wie Supraleitung, Supraflüssigkeit, sehr harte kosmische Höhenstrahlung oder Kugelblitz geben können, wenn man nur erst den neuen Standpunkt fest genug untermauert haben wird.



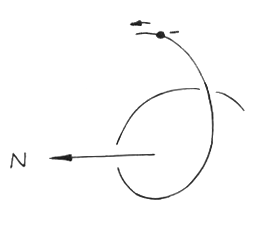
Aber noch mehr kann man vielleicht in Zukunft aus einer solchen Theorie herauslesen: Die laufende Zunahme der Entropie der Natur ist ja eines der wichtigsten Ergebnisse der klassischen Theorie. Nun aber erblicken wir in der Welt der Teilchen (statt des diffusen Bildes eines „zufälligen”, „wahrscheinlichen” undurchdringlichen Dickichts) eine Welt höchster Ordnung und Harmonie, die Welt der eigenen Wechselwirkung. Dieser Welt ist jede Unordnung fremd und deshalb müssen all die Systeme, die sich vorwiegend aus Systemen eigener Wechselwirkung zusammensetzen, eine laufend abnehmende Entropie haben. Das könnte das Gesetz des Darwin sein (die Entstehung des Lebens und die Entwicklung aller biologischen Systeme vom Niederen zum Höheren). Die Natur ist demnach nicht nur kausal, sondern vermutlich auch symmetrisch, vielleicht reicht sogar ein solches ordnendes Prinzip bis in die Fernen des Weltalls und regiert den Aufbau von Fixsternen? Wir wagen an dieser Stelle nicht, Vermessenes zu fixieren, aber vielleicht hält dieses Ordnungsprinzip dem prophezeiten „Wärmetod” das Gleichgewicht?

Eines allerdings ist außerordentlich bedrückend: „Wir haben unsere eingangs gestellte Frage nicht mal andeutungsweise beantworten können und stehen nun immer noch vor dem großen Rätsel: Was ist ein Photon, wie entsteht es und wie vergeht es?

Aber gerade diese Frage, die uns eigentlich erst die vielen kleinen Freuden unserer Entdeckungsreise bescherte, dürfen wir nicht ohne einen einigermaßen ernsthaften Versuch der Beantwortung fallen lassen und setzen noch einmal unsere Bemühungen fort:

Diese Bemühungen gipfeln letztendlich in einer Erweiterung des Magnetfeldsatzes, was wir schon weiter oben ankündigten. Wir betrachten also nun die nebenstehende Abbildung: Eine negative Ladung beschreibt eine Raumkurve, die dem Magnetfeldsatz in der dem Pfeil entsprechenden Richtung genügt (Abb. 45). Dann ist nach der „rechten Hand-Regel” der Nordpol des Magnetfeldes in Pfeilrichtung zu suchen. Nun lassen wir eine positive Ladung in der gleichen Richtung umlaufen (Abb. 46), dann muss der Nordpol nun in umgekehrter Richtung stehen. Wir bemerken, dass zur positiven Ladung die „linke Hand-Regel” gehört. Positive Ladungen erzeugen also Raumwirbel, die einem Links-Koordinatensystem zugeordnet sind, negative Ladungen erzeugen Raumwirbel, die einem Rechts-Koordinatensystem zugeordnet sind.



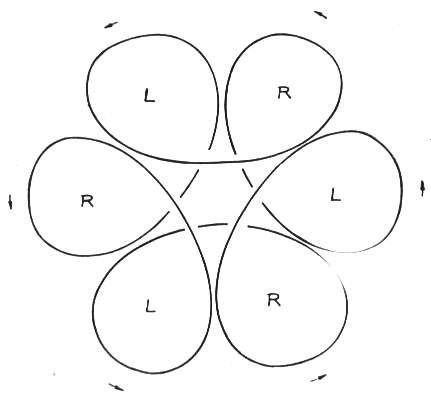
Das ist noch nichts Neues, aber nun wird es interessant: Wir hatten (kurz nach der Berechnung des Planck´schen Wirkungsquantums) eine anschauliche Erklärung des Mechanismus der eigenen Wechselwirkung gegeben und dabei versäumt, die Richtung zu untersuchen, die senkrecht auf der Ebene des Wirbels steht. Es ist aber jedem Betrachter vollständig einleuchtend, dass ein Abdrängen der Feldlinien nach dem konvexen Teil der Bahn nur in einer Richtung - nämlich in der Vorwärts-Bewegungsrichtung der Ladung erfolgen kann. Der magnetische Raumwirbel gleicht also - je nach Vorzeichen der erzeugenden Ladung - einer Schraube mit Rechts- bzw. Linkswindung. Nun betrachten wir unser Protonenmodell in Spinrichtung (Abb. 47). Wir müssen feststellen, dass die einzelnen Rosettenblätter in solch einer Richtung umlaufen werden, dass die Ladung abwechselnd eine Rechts- bzw. eine Linksschraube beschreibt. Sollte etwa ein fremdes Elektron, das wir als Messsonde benutzen, so „halbblind” sein, dass es nur die Bewegung des Positrons wahrnimmt, die zu dem (ihm eigenen) Rechtssystem passt? Vielleicht ist die gesuchte Erweiterung des Magnetfeldsatzes etwa diese?

Ein solcher Satz wäre ohne weiteres anschaulich, denn wenn zwei Magnetfelder mit Rechts- und Linkssystem aufeinander treffen, ist ungefähr ein ähnliches Problem gegeben, als wollte man eine Mutter mit Rechtsgewinde auf eine Schraube mit Linksgewinde aufschrauben.

Nun ist für eine Ladung, die sich im Zustande der eigenen Wechselwirkung befindet, diese Bedingung auf jedem Teil der Bahn erfüllt. Dagegen ändert sich sofort alles, wenn wir fremde Wechselwirkung diskutieren, denn nun ist es entscheidend, welchem Bewegungssystem die „erzeugende” und die „messende” Ladung angehören. Da aber sämtliche Messungen in der Teilchenphysik auf die Bewegungen der Elektronen zurückgeführt werden müssen (denn diese stehen zum Messen zur Verfügung) - oder an deren Bewegung als Eichnormal verglichen werden, könnte man mit Recht vermuten, dass bei einem Modell, das zur Hälfte einem Rechts- und zur Hälfte einem Linkssystem angehört, auch nur die Hälfte der erwarteten Wechselwirkung eintritt. Vielleicht ist dies der tiefere Sinn des Wortes Spin?



Selbstverständlich liebäugeln wir mit einer solchen Auffassung, denn wir wissen ja schon, dass die „Berechnung” des gyromagnetischen Verhältnisses des Elektrons falsch sein muss (wegen der darin vorkommenden Ruhemasse) und wir betrachten es lediglich als einen glücklichen Zufall, dass die damals durchgeführten Plausibilitätsbetrachtungen zum richtigen Ergebnis führten.
Aber schon wieder deutet sich eine jener Verzweigungen an (z.B. die Berechnung des magnetischen Momentes von Proton und Neutron) und wir brechen deshalb hier ab und kehren zum Lichtquant zurück. Es stellt ein Teilchen der Ruhemasse Null dar. Jetzt stehen wir am Scheideweg und wir erläutern deshalb beide Möglichkeiten ausführlich.

Erste Möglichkeit: Ein Teilchen der Ruhemasse Null kann es nach unseren bisherigen Formulierungen nicht geben, denn alle stetig geschlossenen knickfreien Bahnen auf Kugeloberflächen - oder Ellipsoidenflächen, die unseren 5 Forderungen entsprechen, müssen irgendwann einmal „umkehren”. Damit wird sich immer mindestens eine Raumrichtung finden lassen, in der ein fremder Beobachter Rechts- und Linksdrall bemerken und damit eine Masse (lies: potentielle, magnetische Energie, von außen her betrachtet) entdecken kann. Da wir aber bei der Berechnung unseres Wirkungsquantums davon ausgegangen sind, dass Lichtquanten Produkte eigener Wechselwirkung sein sollen, wäre demnach alles falsch, womit wir uns nur ungern abfinden.

Zweite Möglichkeit: Unsere Forderung, dass eigene Wechselwirkung nur auf Kugeloberflächen oder Ellipsoidenflächen möglich sein soll, ist zu starr und muss erweitert werden. Tatsächlich ist sie ja auch aus der Forderung der Konstanz des Absolutwertes des Drehimpulses entstanden und es scheint, dass diese Forderung allgemeiner Natur ist.





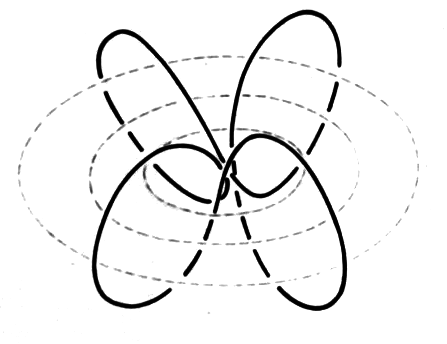
Es ist nämlich ohne weiteres nicht im Widerspruch zur Forderung der Konstanz des Absolutwertes des Drehimpulses, (wenn wir ausnahmsweise noch einmal die „klassische” Vorstellung benutzen); wenn wir eine Raumkurve für das Feld des Photons einführen, die auf einer zum Ring gekrümmten Zylinderoberfläche liegt. (Siehe nebenstehende Abbildung 48).

Jetzt erblicken wir in „Spinrichtung” einen Toroiden, der ja durch seine außerordentlich gute Abschirmung des Magnetfeldes nach außen bekannt ist. Damit ist hier die Möglichkeit offen, ein Teilchen der Ruhemasse Null einzuführen, ja mehr noch: Gerade dieses Teilchen kann vielleicht noch einmal sehr anschaulich die Existenz von Antimaterie deutlich machen, denn man kann einen Toroiden linksherum und rechtsherum aufwickeln. Sollte vielleicht das „ominöse” Neutrino das Photon der Antimaterie sein? Sollte dieses Teilchen einem Feldverlauf entsprechen, der einem linksgewickelten Toroiden zugeordnet ist? Sind etwa auf die freien elektromagnetischen Felder in der Lage, Selbstinduktion zu zeigen? Sind diese Felder vielleicht vergleichbar mit einer idealen Flüssigkeit, in der freie Raumwirbel entstehen und vergehen können (eben weil der Helmholtz´sche Wirbelsatz nur für konservative Kräfte in einer solchen Flüssigkeit Gültigkeit hat, denn bei eigener Wechselwirkung sind konservative Kräfte nicht mehr vorstellbar)? Fragen über Fragen, deren Beantwortung der Verfasser nicht mehr gewachsen ist und die an alle Leser gerichtet sein sollen.


Verzeichnis der verwendeten Literatur:

1. Joos, G. „Lehrbuch der theoretischen Physik” 10. Auflage, Akademische Verlagsgesellschaft, Geest & Portig K.-G., Leipzig 1959
2. Grimsehl, „Lehrbuch der Physik” Bd. I bis IV B.G., Teubner Verlagsgesellschaft, Leipzig 1964
3. Gehrtsen, Ch., „Physik, ein Lehrbuch zum Gebrauch neben Vorlesungen” Springer-Verlag, Berlin, Göttingen, Heidelberg 1958
4. Heber - Weber, „Grundlagen der modernen Quantentheorie” Teil 1, B.G. Teubner Verlagsgesellschaft, Leipzig 1964
5. Westphal, W.H. „Physik - ein Lehrbuch” 20. u. 21. Auflage, Springer-Verlag, Berlin, Göttingen, Heidelberg 1959
6. Bronstein/Semendjajew, „Taschenbuch der Mathematik” B.G. Teubner Verlagsgesellschaft, Leipzig 1962

Previous Next