Diese Funktion kann man nun recht mühelos graphisch integrieren und erhält:

  XXXVII  

Daraus folgt für :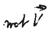

Nun, da alle Größen auf den Kreis zurückgeführt sind. können wir berechnen:

  XXXVIII  

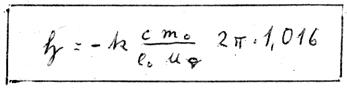
Zwei interessante Ergebnisse wollen wir zunächst nur registrieren: Erstens erscheint das -Feld ohne Quantenzahl, denn diese kürzt sich nach der Integration heraus. Ebenfalls stehen in dieser Gleichung nun außer nur noch Konstanten. Das ist die mathematische Formulierung unseres Magnetfeldsatzes. Ein Elektron kann bei irgendeinem Umlauf nur ein Magnetfeld erzeugen, dessen Stärke im Wesentlichen nur von dem Weg, den das Elektron abläuft, abhängt. Dabei darf nur der Teil des Weges zur Erzeugung des -Feldes beitragen, der eine stetige und in der räumlichen Ableitung stetige geschlossene Raumkurve umschließt