Den Ausdruck, der auf der rechten Seite in der Klammer steht, nennen wir S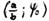. Diese Funktion S 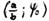ist stetig über 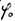und besitzt keine Unstetigkeitsstellen bezüglich ihrer Ableitung nach 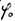. Sie ist allerdings nicht mehr elementar ausdrückbar. Jedoch lässt sie sich sehr bequem graphisch erzeugen, wenn man die Ellipse und den dazugehörigen umbeschriebenen Kreis aufzeichnet und die in der Abbildung 20 angegebenen Strecken ausmisst.

  XXXVI  

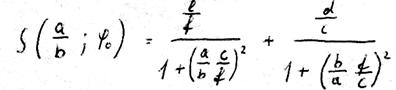
Für unseren Fall der Größen a und b ist sie eine wenig von 1 verschiedene Größe, die sinusähnlich verläuft.

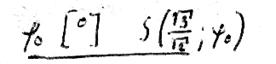0	1,0
10	1,0024
20	1,0065
30	1,097
40	1,0130
50	1,0270
60	1,0130
70	1,0085
80	1,004
90	1,0