Now, this function can very easily be graphically integrated and we obtain:

  XXXVII  

For 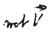we obtain:

Now all terms have been reduced to the circle and we can calculate :

  XXXVIII  

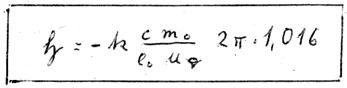
Initially, we just want to notice two interesting results: First, the field appears without quantum number because this is cancelled after integration.
Further, apart from , there remain only constants in the equation. This is the mathematical formulation of our magnetic field theorem. In any revolution, one electron can generate only one magnetic field the strength of which mainly depends only on the trajectory travelled by the electron. Thereby only that part of the trajectory that encloses a continuous and in the spatial derivative closed continuous space curve. may contribute to the generation of the field.