Daraus folgt für den Nenner der linken Seite:

  IX  

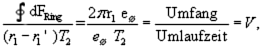
eine Umlaufgeschwindigkeit auf einer festen Bahn. Das ist verblüffend!
Setzen wir nun in Gleichung VII z = 1 und vergleichen beide Nenner, so steht nun da:

  X  

auf der innersten Bahn des Wasserstoffatoms!

Nun kommen wir zu der entscheidenden Frage, denn alles das, was bisher aufgeschrieben wurde, diente zur Erarbeitung der nun folgenden Sätze. Wir fassen zusammen (unter der Voraussetzung, dass unsere bisherigen Vermutungen einen wahren Kern enthalten): Liegt der Atomkern innerhalb der zu integrierenden Fläche, dann wird Licht emittiert (oder absorbiert). Liegt dagegen der Kern nicht in dieser Fläche, dann haben wir es mit einer festen Bahn zu tun. Warum also integriert man nicht in jedem Falle über den Kern?

Da wir schon weiter oben die Fläche mit dem Magnetfeld identifizierten, behaupten wir nun:

Das Magnetfeld, das ein Elektron bei einem Umlauf auf einer stationären Bahn (die der Quantenbedingung genügt) erzeugen sollte, ist am Kern einfach Null, es ist nicht da. Wenn aber das Magnetfeld am Kern nicht da ist, kann natürlich solch ein Elektron bei seinem Umlauf nicht strahlen, muss also auf einer stabilen Bahn bleiben, denn zum Abstrahlen von Lichtquanten braucht man ein elektrisches und ein magnetisches Feld. Vielleicht läuft also das Elektron auf einer Bahn um den Kern, die so geartet ist, dass am Kern einfach kein Magnetfeld entsteht. Da aber der Kern durch die Coulomb-Anziehung das Elektron auf eine Kreisbahn oder Ellipse bannt, gibt es für die Auswahl verschiedener Bahnkurven zunächst gar keine Möglichkeit, irgendwie anders geartete Bahnen als Kreise oder Ellipsen zuzulassen.