So the denominator of the left side of the equation becomes:

  IX  

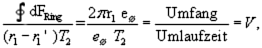
a rotational speed within a steady orbit. This is amazing!
Now, let's insert z = 1 (VII) into the equation and compare the two denominators. We obtain:

  X  

on the innermost orbit of the hydrogen atom!

Now we come to the decisive question, since everything that has been written down until now has been used to elaborate the following statements. To sum up (under the condition that our speculations so far are basically true): if the atomic nucleus is within the area to be integrated, light will be emitted (or absorbed). However, if the nucleus is not located within this area, we will have a steady orbit. Hence, why not always integrate over the nucleus?

Since we have identified the area as the abovementioned magnetic field, we now claim:

The magnetic field that should be generated by an electron during its movement within a stationary orbit (meeting the quantum condition), is simply zero at the nucleus, i.e. there isn't any magnetic field. If, though, the magnetic field does not exist at the nucleus, then such an electron cannot radiate on its orbit, and must therefore remain on a stable orbit. This is because an electrical field and a magnetic field are required, when a light quantum is emitted. Thus, maybe the electron moves around the nucleus on an orbit, that simply does not generate a magnetic field at the nucleus. But because the nucleus fixes the electron on a circular or elliptic orbit due to the Coulomb attraction, it is not possible for the moment, to allow for the selection of orbits other than circles or ellipses.