XLV  

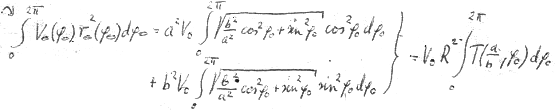
T ist nun ebenfalls eine nicht mehr elementar integrierbare elliptische Funktion
- genau wie S. Man kann sie aber ebenfalls recht bequem graphisch integrieren. In unserem Fall der Größen a und b erhält das Integral die Größe 0,50077 * 2π Es ist also eine - wenig von π verschiedene Größe.

Daraus folgt:

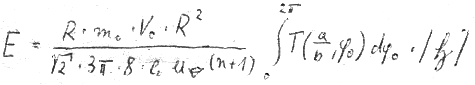
Nun kommen wir zu dem schon erwähnten Schönheitsfehler von :
Es existiert keine Komponente von in der Ebene der Fläche F, sondern steht auf dieser Fläche senkrecht. Der Poyntingvektor ist aber für Energieströmungen gültig, bei denen und eine Komponente in der Ebene der Fläche F haben. Nun, wir nehmen diese Eigenart der „Teilchenwelle” zunächst zur Kenntnis und rechnen mit der Komponente von weiter, die uns zur Verfügung steht. Wir sind sonst nämlich gezwungen, den Magnetfeldsatz als falsch zu bezeichnen - und gerade dieser hat uns eine Serie von schönen Indizien für die Richtigkeit unseres Weges beschert. Andererseits sehen wir auch kein Argument, dass man unbedingt bei einem geladenen Teilchen genau die gleichen Vorschriften zu erwarten hat wie bei Photonen, denn noch wissen wir zu wenig über die Mechanismen, die nicht mehr streng herleitbar sind und - wir sagten es einleitend - gewisse Willküren sind bei unserer Verfahrensweise unvermeidbar.