XLV  

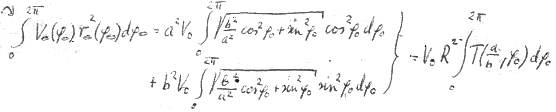
Now T, like S , is not an elementarily integratable elliptic function.
But it can be easily integrated graphically, too. In our case of the quantities a and b the integral takes on the value 0.50077 * 2π It is thus a variable differing slightly from π.

Hence:

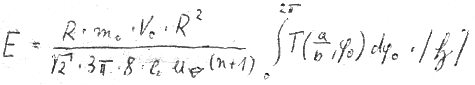
Now, let’s proceed to the aforementioned minor draw-back of :
There is no component of within the plane of the area F but is perpendicular to this area. However, the Poynting vector is valid for energy fluxes for which and have a component within the plane of the area F. So, we first take note of this characteristic feature of the “particle wave” and continue calculating with the available component of Otherwise, we would be forced to declare the magnetic field theorem wrong – and it was precisely this theorem that brought us a series of nice indications for the validity of our approach. On the other hand, we do not see any reason why we have to expect absolutely the same rules for a charged particle as for photons because we still know too little about the mechanisms that cannot be strictly derived and, as we mentioned at the start, certain arbitrary acts cannot be avoided with our procedure.