Wir schreiben deshalb für die Fläche F (die wir selbstverständlich mit der Fläche der Ellipse in Richtung 1 identifizieren) unsere bewährte Integralform und verfahren in der gleichen Weise mit diesen Größen wie bei der Behandlung von ns:
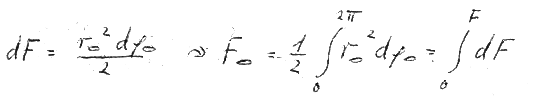
(Abb. 22)
Da aber V0 eine Variable von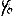 
ist, gehört sie - bei eigener Wechselwirkung eines Teilchens mit sich selbst - unter das Integral - und die Schwierigkeit der Variabilität von V0 und damit von E ist überwunden:
XLIV
Wir drücken nun in üblicher Weise die elliptischen Funktionen durch Größen der Kreise aus:
