But now let's return to our quantum number to be selected for the field. After all, we must not select it equal to n magn., because we have required self-interaction to occur only if the electron has already terminated one revolution, i.e. that a magnetic field already exists. Hence:

Hence, we can write for the equations XXVII and XXVIII::

  XXXI  

  XXXII  

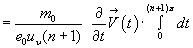
But we are not satisfied even with these equations since there are functions of time (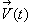) in front of the integrals. While this notation may certainly be correct for the summation over many electrons (with superconduction), it is wrong for one single electron. Therefore, we must require that - if the particle is to interact with itself - all terms dependent on t be part of the integrals. Thereby with the -field, the differentiation and the integration over t offset each other because V on the ellipse only depends on t; i.e. the partial differential and the total differential as a function of time are identical. This notation is not arbitrary since certainly is a function of the location in the superconductive material if we consider many electrons. (It is known that the interior of the supercrystal is shielded by a "supercurrent" flowing on its surface.)