Therefore, we examine an electron on the crystal surface:

  XXXIII  
=

  XXXIV  

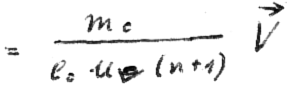
If we look at these two equations and keep in mind that the product of and must appear when calculating the energy - that we actually want to provide at some point of our calculation - then the term n (n + 1) would appear in the denominator of this product!
This may be the reason why the term must stand for the square of the angular momentum in quantum theory! Actually, we have provided an illustrative interpretation earlier: self-interaction is only possible if one revolution has already been performed (due to the magnetic field theorem). We assess this numbers game again as an indication of the validity of our approach and now start calculating the magnetic field according to equation XXXIII. We notice with satisfaction that, unlike the Biot-Savart law, this magnetic field is not branded by the disadvantage of the impossibility of the expected results.

Yet another small correction is necessary in this equation, and as usual we explain it by using the magnetic field theorem: in the following, we will not adopt τ as the total time needed by the electron to follow its "wobble trajectory" but only as the revolution period for the ellipse visible in direction 1 since there is no magnetic field beyond this continuous and in the spatial derivative continuous space curve! The same holds truefor calculating only for this ellipse while not considering the other parts of the trajectory.

Therefore, we write:

  XXXV