Doch nun sind wir verpflichtet, das gyromagnetische Verhältnis des Einstein- de Haas-Versuches für unser Spinmodell auszurechnen, um zu zeigen, dass dieses Modell auch hier Übereinstimmung mit den tatsächlich gegebenen Werten liefert:

  XII  

    Das magnetische-Moment ist (gemittelt über die Dauer eines Umlaufes):

Daraus folgt:

  XIII  

Der Drehimpuls (ebenfalls über einen Umlauf gemittelt) ist:

  XIV  

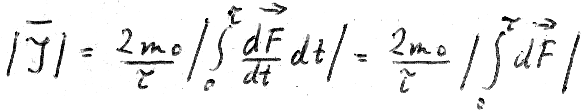
auf Wir behaupten nun, dass das Integral 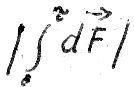gleich 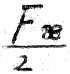ist.

Man kann diesen Beweis auf verschiedene Weise führen, z.B. dadurch, dass man die Tatsache berücksichtigt, dass der (gemittelte) Drehimpuls sich aus zwei Drehungen zusammensetzt: Eine Vorwärtsdrehung innerhalb jedes Quadranten und eine Rückwärtsdrehung beim Wechsel von einem Quadranten in den anderen. Wir führen den Beweis mit Hilfe einer sehr anschaulichen Hilfsbahn. Wir können nämlich die angegebene Bahn durch drei einzelne Bahnen ersetzen, deren mittlerer Drehimpuls sich sofort aus der Bahnkurve ablesen lässt, so dass wir ohne große mathematische Hilfsmittel auskommen. Der erste Teil dieser Bahn ist in der Abbildung 11 angegeben.