Nevertheless, we are obliged to calculate the gyro-magnetic ratio of the Einstein-de-Haas experiment for our spin model to show that this model also corresponds here to the actually given values:

  XII  

    The magnetic moment is (in terms of the average of the period of a single revolution):

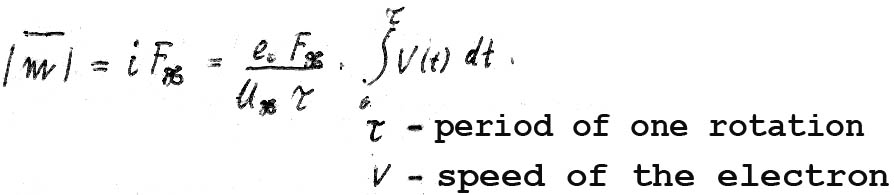
We obtain:

  XIII  

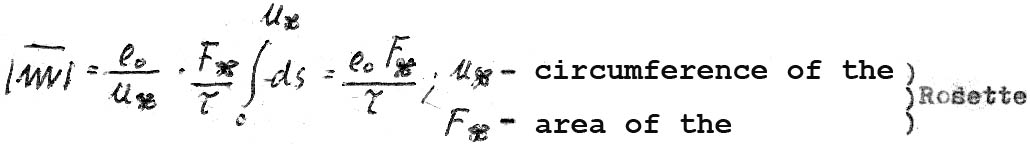
The angular momentum (also in terms of the average of the period of rotation) is:

  XIV  

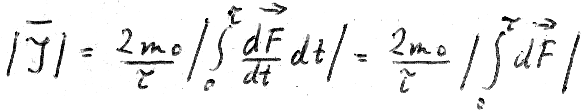
Based on this, we can claim that the integral 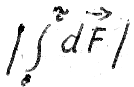equals .

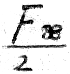One can prove this in two different ways, e.g. by considering the fact that the (mean) angular momentum is composed of two rotations: one forward rotation within each quadrant and one backward rotation when changing from one quadrant into another. We provide this proof by means of a very illustrative auxiliary orbit. This orbit may be substituted by three single orbits whose mean angular momentum can immediately be read from the orbital curve so that we can do without complicated mathematical equations. For the first part of this orbit see Fig. 11.