This amount of energy given in equation XLIII only exists for one eighth of the complete revolution of the electron around the nucleus. And this eighth is only an approximation, as well. When calculating more precisely, we should change the integration limits in equation XLII continuously and then average the result. Since in our model this error can only be insignificant (all ellipses are not strongly "elliptic") we are satisfied with this one eighth.

However, for the Poynting vector exactly the energy is calculated that flows through the area F per unit time (e.g. per second). Therefore, we have to divide the right side of the equation by 8 too:

Now we come to use und and, for sake of clarity, write the equations XXXIX and XL as follows:

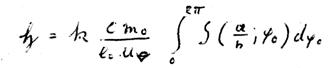
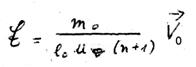
Anyway, the two quantities have some minor drawbacks. First, we will discuss the drawback of suggested above: is not a constant but for our case we demand E = const! This is because we, according to our expectations about a self-interaction quantum, have to set E = const since we want the law of conservation of energy to be valid also within the range of self-interaction. Secondly, we have to set E = const, if we want to take the modest perpetuum mobile of superconduction into account.