First, we replace the speed of light in the propagation direction of the wave by the speed of the particle in direction 1. We call this component Vz. Now, we look toward b-d and draw only that part of the orbit that is necessary to generate a closed ellipse visible in direction 1 (Fig. 21):

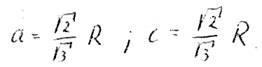
Hence, for Vz:

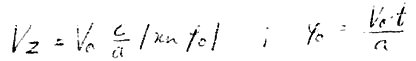
This equation is an approximation of Vz. Strictly speaking, again this should be an elliptical function which, though, does not deviate considerably from the proposed approximation.

Next, for the equation of the Poynting vector we write:

  XLII  

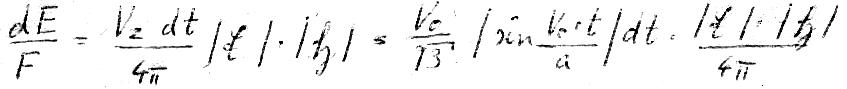
And after the integration over 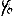from 0 to 2π (due to the magnetic field theorem):

  XLIII  

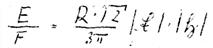
We now have the energy that would flow through the area F if only this ellipse were continuously travelled. This, however, is not true because in our model there are definitely points of time at which we do not find any energy in direction 1. This is the case when the electron travels those parts of the orbit that should not provide a contribution of energy.