We also rewrite the second (we do not make too serious an error if we accept only integral numbers of revolution):
1 second ≈ number of the revolution periods * revolution period

  XXX  

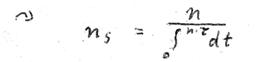
Now, since we do not want to sum up many electrons, we will use another concept that enables us to express n_s for one electron. For this purpose we provide the following example: If each of 6 electrons performs one revolution per second, the following equation will apply: .

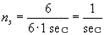The result will be the same if one electron is made to orbit six times faster:

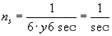
This is what we have achieved: we consider the number n as a number of revolutions that can be performed by one electron in a defined period and now require this number to be an integer. We justify this requirement by our magnetic field theorem that forbids the discussion about the existence of a magnetic field at all unless at least one complete revolution has been performed. Thus, we have illustratively introduced the main quantum number n.

Thus, we write:

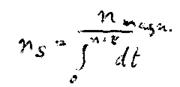
Consequently, this equation should apply also for magnetic fields.