Now we equate the Lorentz' force with the centrifugal force on the small circular paths:

  XXIV  

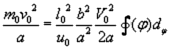
  XXV  

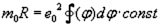
So, and now we give free rein to our imagination:

We assume that 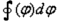contains ambiguous solutions and that it is a linear function of 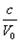because then a quantum rule would be established:

  XXVI  

This would mean that 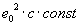could apply! If we calculate the numerical value of 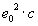, we will see that it is only about 3 powers of ten away from the value of Planck's constant. Nevertheless all of these speculations are only built on sand; now let's eliminate the errors and learn from the defeat.

We have reached the point to formulate the decisive theorem:

The Biot-Savart law is useful for calculating a magnetic field from any current-flow in a conductor loop. But how do we find its strength, direction etc.? For sure we will find it by measuring the effect of this magnetic field on any other magnet or at least a charge e₀ But as we know that molecular magnets do not exist, the use the Biot-Savart law requires at least two electrons: one electron that generates the field and a second whose changes are still to be determined. Thus, the Biot-Savart law describes the dependencies of at least two electrons to each other (as practically all laws of physics are designed to examine cause and effect on different objects).